Основні види моделювання

Вимоги до моделей

У загальному випадку під час побудови моделі потрібно враховувати такі вимоги:

v незалежність результатів розв'язання задач від конкретної фізичної інтерпретації елементів моделі;

v змістовність, тобто здатність моделі відображати істотні риси і властивості реального процесу, який вивчається і моделюється;

v дедуктивність, тобто можливість конструктивного використання моделі для отримання результату;

v індуктивність — вивчення причин і наслідків, від окремого до загального, з метою накопичення необхідних знань.

Оскільки модель створюється для вирішення конкретних завдань, розробник моделі має бути впевненим, що не отримає абсурдних результатів, а всі одержані результати відображатимуть необхідні для дослідника характеристики та властивості модельованої системи.

Модель повинна дати можливість знайти відповіді на певні запитання, наприклад: «що буде, якщо...», оскільки вони є найбільш доцільними під час глибокого вивчення проблеми. Не варто забувати, що системні аналітики використовують модель для прийняття рішень і пошуку найкращих способів створення модельованої системи або її модернізації. Завжди потрібно пам'ятати, що користувачем інформації, отриманої за допомогою моделі, є замовник. Недоцільно розробляти модель, якщо її не можна буде використовувати. Більш того, робота з моделлю має бути автоматизованою для замовника до такого ступеня, щоб він міг працювати з нею в межах своєї предметної області. Таким чином, між моделлю і користувачем повинен бути розвинутий інтерфейс, який звичайно створюється за допомогою системи меню, налагодженої на застосування моделі в певній галузі.

Ступінь деталізації моделі потрібно вибирати з огляду на цілі моделювання; можливості отримання необхідних вхідних даних для моделі; з урахуванням наявних ресурсів для її створення. Відсутність кваліфікованих фахівців може звести роботи зі створення моделі нанівець. З іншого боку, чим детальніше розроблено модель, тим вона стійкіша до вхідних впливів, які не були передбачені під час проектування, і на більшу кількість запитань може дати правильні відповіді.

Єдина класифікація видів моделювання неможлива через багатозначність поняття моделі в науці, техніці, суспільстві. Широко відомими видами моделювання є комп'ютерне, математичне, імітаційне та статистичне.

Комп'ютерне моделювання визначимо як реалізацію моделі за допомогою комп'ютера. Особливістю комп'ютерного моделювання є його інтерактивність, що дає змогу користувачу втручатися в процес моделювання та впливати на результати завдяки узгодженості дій користувача і моделі, яка відтворює об'єкти реальногосередовища або гіпотетичні події та процеси. Під час комп'ютерного моделювання може бути задіяно реальні об'єкти (наприклад, кабіна пілота), віртуальні об'єкти, згенеровані комп'ютером, які відтворюють реальні об'єкти (наприклад, потоково-конвеєрна лінія для збирання автомобілів). Інтерактивне комп'ютерне моделювання широко застосовується в навчальних системах, наприклад для побудови тренажерів і в ситуаційних іграх.

Що стосується математичних моделей, або математичного моделювання, то слід відзначити, що під час їх використання багато чого залежить від способу подання як моделі, так і результатів моделювання. Розглянемо простий приклад. Нехай на деякому підприємстві для водопостачання використовується резервуар, об'єм якого становить W тисяч літрів. Рівень споживання – V _П тисяч літрів, а швидкість наповнення резервуара – V _З тисяч літрів за добу. Необхідно знайти час Т, за який буде заповнено резервуар. Схему цієї системи зображено на рис. 1.4, де резервуар позначено прямокутником, а вхідний і вихідний потоки – стрілками з «вентилями», які регулюють ці потоки. Хмарки позначають необмежені потоки. Такі ідеограми широко використовуються під час побудови моделей неперервних процесів.

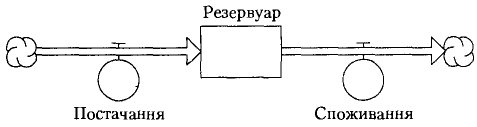
Рис. 1.4. Схема системи водопостачання

Знайдемо час заповнення резервуара:

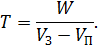
(1.1)

Ця математична модель процесу наповнення резервуара є надто ідеалізованою, тому що всі її параметри вважаються незмінними в часі, зовнішні впливи на систему не враховуються. Завдяки такій ідеалізації маємо дуже просту модель, яка дає змогу розв'язати задачу аналітично. Однак за допомогою такої моделі можна отримати відповідь тільки на одне конкретне запитання — за який час буде заповнено резервуар.

Якщо задачу наблизити до практики, то, будуючи модель, необхідно враховувати, що потреби підприємства у водопостачанні постійно змінюються, більш того, можливі перебої в роботі насосів під час подавання води. Розв'язок задачі в частково замкнутому вигляді можна записати як

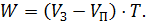
(1.2)

За рахунок неявного запису отримано більш придатну для дослідження та аналізу реальних процесів математичну модель. Час заповнення резервуара об'ємом W залежить від параметрів моделі , . Використання цієї моделі дає можливість вивчити відношення між величинами і , якщо задавати різні початкові значення для них, і побудувати графік наповнення резервуара (рис. 1.5).

Рис. 1.5. Графік наповнення резервуара

Реалізувати цю модель можна за допомогою і чисельних методів. Змінюючи у формулі (1.2) значення t від 0 з деяким кроком D t до такого, що буде виконуватись рівність, отримаємо динамічну характеристику заповнення резервуара. Чим менший крок D t, тим точніший отримаємо результат, але тим довше буде вирішуватись задача моделювання.

Термін «моделювання» відповідає англійському слову «modeling», тобто побудові моделі та її аналізу. Англійський термін «simulation» відповідає прийнятому терміну «імітаційне моделювання», але часто вони використовуються разом, коли йдеться про технологічні або системні етапи моделювання, пов'язані з прийняттям рішень за допомогою моделей.

Імітаційне моделювання – це метод конструювання моделі системи та проведення експериментів. Однак під таке визначення підпадають майже всі види моделювання. Тому потрібно виділити суттєві особливості імітаційного моделювання.

Перш за все слід подати в моделі структуру системи, тобто загальний опис елементів і зв'язків між ними, потім визначити засоби відтворення в моделі поведінки системи. Здебільшого поведінку системи описують за допомогою станів і моментів переходів між ними. Стан системи в момент часу t визначають як безліч значень певних параметрів системи у цей самий момент часу t. Будь-яку зміну цих значень можна розглядати як перехід до іншого стану. І врешті-решт, імітаційна модель має відобразити властивості середовища, в якому функціонує досліджувана система. Зовнішнє середовище задають вхідними впливами на модель.

Вся інформація про імітаційну модель загалом має логіко-математичний характер і подається у вигляді сукупності алгоритмів, які описують процес функціонування системи. Отже, здебільшого імітаційною моделлю є її програмна реалізація на комп'ютері, а імітаційне моделювання зводиться до проведення експериментів з моделлю шляхом багаторазового прогону програми з деякою множиною даних — середовищем системи. Під час імітаційного моделювання може бути задіяно не тільки програмні засоби, але й технічні засоби, люди та реальні системи.

З математичної точки зору імітаційну модель можна розглядати як сукупність рівнянь, які розв'язують з використанням чисельних методів у разі кожної зміни модельного часу. Окремі рівняння можуть бути простими, але їх кількість і частота розв'язання — дуже великими. Розв'язання таких рівнянь під час імітаційного моделювання означає встановлення хронологічної послідовності подій, які виникають у системі і відображають послідовність її станів. Отже, імітаційна модель функціонує так само, як система.

Якщо повернутись до процесу наповнення резервуара (рис. 1.6), то за допомогою імітаційної моделі весь процес можна відтворити з використанням рівняння (1.2). Позначимо через W_i поточний стан резервуара, який відтворюється в певні моменти модельного часу, що змінюється з постійним кроком D t:

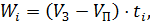
(1.3)

де t_i = t_{i +1} + D t (і = 1, 2,...), t ₀ = 0. Така модель є детермінованою. Процес моделювання закінчується, якщо на деякому кроці виконується умова W £ W_i, тобто розв'язок отримуємо за один прогін імітаційної моделі. Точність результату буде залежати від значення D t.

Рис. 1.6. Динамічна характеристика наповнення резервуара

За наявності в моделі випадкових факторів виникає необхідність статистичного оцінювання результатів моделювання, що виконується за допомогою методу статистичного моделювання (методу Монте-Карло). Статистичне моделювання є самостійним видом моделювання, яке включається в імітаційне моделювання тільки за необхідності моделювання ймовірнісних систем і процесів.

Побудуємо більш реальну модель системи, яка розглядалась вище. Припустимо, що рівень споживання води на підприємстві має імовірнісний характер і змінюється згідно з рівномірним розподілом імовірності в межах V _П ± DV_П. Тоді значення V _П у деякий момент часу t_i будемо визначати як

2DV_П´ r_i + V _П – DV_П,

де r_i — випадкове число, рівномірно розподілене в інтервалі [0, 1].

Результати роботи імітаційної моделі наведено на рис. 1.7. У цьому випадку після кожного прогону моделі отримаємо випадкові значення T_j, де j – кількість прогонів, j = 1, 2, 3 …

Для кожного прогону потрібно задавати свою послідовність випадкових чисел r_i. Як видно на рис. 1.7, отримані значення T_j будуть відрізнятись від середнього значення Т, знайденого за допомогою детермінованої моделі. Таким чином, щоб оцінити час Т наповнення резервуара, потрібно задати точність оцінювання e = D T і рівень довіри a. Звичайно a = 0,95, тобто є гарантія, що в 95 випадках із 100 середнє значення часу Т буде знаходитись у межах Т ± D T.

Рис. 1.7. Графік реалізації стохастичної моделі

Із вищенаведеного прикладу видно, що стохастичне моделювання використовується під час імітаційного моделювання тільки за необхідності врахування випадкових факторів.

Дата добавления: 2014-01-05