Системна динаміка

Для формального представлення моделей неперервних систем Дж. Форрестер у 1960 році запропонував підхід, названий системною динамікою, який дає змогу будувати моделі динамічних взаємопов'язаних систем за допомогою причинних діаграм циклів і схем виду «фонд – потік». Він же запропонував для числового моделювання таких систем мову Динамо. Модель будується як система диференціально-різницевих рівнянь, а мова Динамо дає можливість автоматизувати процес їх написання. Практично всі сучасні засоби неперервного та неперервно-дискретного моделювання базуються на цій мові для побудови моделей. На відміну від математичного розв'язання системи таких рівнянь у замкненому вигляді використовується числове розв'язання з дискретним кроком часу, що дає змогу моделювати на деякому проміжку часу динамічні зміни фондів, пов'язаних з точкою часу і потоків. Фонди та потоки пов'язані між собою через змінні.

Фонд можна трактувати як деяку кількість чого-небудь, що виміряється в певних одиницях (наприклад, фізичних, грошових та ін.). Фонди можуть акумулювати одиниці фонду. Найкраще їх уявляти як резервуари, ресурси або буфери. Фонди поповнюються через вхідні потоки та спорожнюються через вихідні. Як буфер фонд може використовуватись для забезпечення балансування швидкості накопичення та витрачання.

Потік – це процес, що протікає неперервно в часі, оцінити який можна в деяких кількісних одиницях за певний проміжок часу. Залежно від характеристики використання потоки поділяються на обмежені та необмежені, одно - та двоспрямовані, конвертовані та неконвертовані. Потік, як правило, обмежується фондом. Потоком можна керувати, тобто збільшувати або зменшувати його інтенсивність за допомогою деяких алгебричних виразів.

Існує багато різних способів зв'язувати у динамічних моделях причини та наслідки, не розглядаючи конкретні методи. В їх основі лежить кілька підходів. Розглянемо три з них, які наведено на рис. 1.11.

Рис. 1.11. Три підходи до зв'язування причин і наслідків для побудови моделі

Перший підхід полягає в тому, що наслідок виникає з причини і взаємозв'язок між різними причинами відсутній. Такий підхід, наприклад, використовують бухгалтери під час розрахунків. Як правило, для цього застосовують статичні та статистичні моделі.

Другий підхід передбачає, що між причинами та наслідками існує лінійний зв'язок у вигляді ланцюжка. Такий підхід підтримують інженери та науковці, які вважають, що всі події у всесвіті залежать одна від одної. Маючи достатню кількість інформації, можна побудувати залежності в часі для всіх подій у майбутньому. Системні мислителі, які застосовують цю парадигму, користуються діаграмами впливу та моделями лінійних рівнянь і вважають, що завжди можна логічно прослідкувати, «що є на вході і що буде на виході».

Згідно з третім підходом всесвіт розглядається як система зі зворотними зв'язками, тобто ланцюжки причин і наслідків циклічно пов'язані між собою. Таке уявлення підтримують кібернетики, прихильники нелінійної динаміки та хаосу. Вони вважають, що всесвіт значною мірою хаотичний, і передбачити майбутнє з огляду на його минуле неможливо. Ці системні мислителі використовують циклічні причинні моделі, нелінійні рівняння в кінцевих різницях. Часто поведінка таких моделей далека від реальності та інтуїтивного уявлення і може бути дещо несподіваною для дослідника.

На рис. 1.12 зображено найпростішу причинну циклічну модель для деякої популяції, яка має два цикли. Лівий цикл, позитивний, свідчить про приріст популяції в разі збільшення народжуваності, що у свою чергу збільшує народжуваність. Правий цикл, негативний, свідчить про зменшення популяції у випадку збільшення смертності, що у свою чергу зменшує смертність. Такі пари причинних циклів можуть використовуватись під час побудови більш складних динамічних моделей.

Рис. 1.12. Найпростіша причинна модель циклу популяції

Побудова складних динамічних моделей з використанням причинних циклів включає такі етапи.

1. Абстрагування від фізичної структури.

2. Концентрація на процесах для визначення траєкторій, за якими система починає та закінчує працювати.

3. Використання простих диференціально-різницевих рівнянь для опису процесів у системі:

v 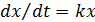— показова функція, яка визначає швидкість зміни фонду в часі, де х — фонд (для прикладу з водопостачанням — це швидкість наповнення бака);

v — сигмаїдальна, або логістична, крива, або S -крива;

або системи рівнянь:

v (наприклад, х — кількість травоїдних тварин);

v 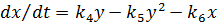(наприклад, у — кількість хижаків).

Такі системи рівнянь відомі як рівняння Ланкастера. їх можна використовувати для дослідження складних взаємозв'язків, конкуренції або конфліктів. За допомогою комп'ютерів подібні рівняння можна подати в числовому вигляді. Для цього використовують прості рівняння рекурсії:

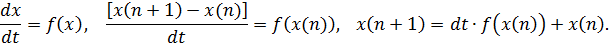
Якщо описати дані рівняння словами, то наступний рівень дорівнюватиме попередньому плюс невеличка зміна протягом короткого проміжку часу. Таким способом можна будувати складні динамічні моделі за допомогою створення простих блоків у вигляді відношень і рівнів. У сучасних пакетах моделювання цей процес запису рівнянь автоматизовано із застосуванням ідеографічних схем.

Причинні діаграми циклів дають змогу провадити якісне моделювання, а діаграми «фонд – потік» — кількісне. Щоб пояснити явище, потрібно знайти «причини» його виникнення. Припустимо, що таку причину визначено і наслідок може спостерігатись кожного разу, коли ця причина присутня. Якщо описують ці концепції системного мислення звичайними словами, то використовують слова або фрази «тому що», «завдяки тому, що», «якщо..., то» та ін. З погляду математики, якщо розглядають функціональну концепцію з однією незалежною змінною, ця змінна — причина, а залежна змінна — наслідок.

У разі кількісного моделювання таких систем модельовані об'єкти — це об'єкти, параметри яких можна виміряти і між якими існують функціональні залежності. Якщо розглядати систему «хижаки – зайці», то в кількісній моделі знищення хижаками деяких зайців — це не знищення тварин, а зменшення їх кількості. Тобто в системі є суттєва різниця між зайцями як тваринами та їх кількістю. Наприклад, вовк може знищити зайців, але кількість вовків не може знищити дещо, а може тільки вплинути на кількість зайців.

Вищенаведені моделі динамічних систем широко використовуються для побудови спеціальних засобів моделювання — мов і пакетів неперервного та неперервно-дискретного імітаційного моделювання.

Дата добавления: 2014-01-05