Міри близькості на метризованих відношеннях

У метризованому відношенні кожен елемент матриці 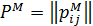відповідає парі (х_i, x_j) Î Р, і його можна змістовно розглядати як ступінь переваги чи подібності альтернатив, а також відносну частоту вибору однієї з альтернатив при попарних порівняннях.

Поділимо метризовані відношення на два класи відповідно до їх подання у вигляді матриці – клас метризованих відношень порядку та лінійного порядку та 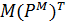– клас метризованих відношень толерантності й еквівалентності.

Будемо вважати, що матриці метризованих відношень узгоджені.

Матриця адитивного метризованого відношення буде узгодженою, якщо для всіх елементів виконується умова: (вважаємо, що 0 = –0 та q = –q). Відповідно матриця метризованого відношення буде узгодженою, якщо для всіх елементів .

Отже, якщо матриці метризованих відношень узгоджені, то в класі 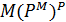для визначення відстані достатньо розглядати такі елементи матриці, для яких (x_i, x_j) Î Р, а для толерантностей і еквівалентностей – такі, що (x_i, x_j) Î Р, в обох випадках і £ j. Тому надалі віддаль між метризованими відношеннями будемо визначати на цих підмножинах елементів матриці Р^M.

Міра близькості на метризованих відношеннях повинна задовольняти аксіоми 1–4, введені раніше для ранжувань, причому поняття «між» для аксіоми 3 вводиться для метризованих відношень наступним чином. Вважатимемо, що метризоване відношення Q знаходиться між метризованими відношеннями Р та R, якщо виконуються наступні умови:

Наступну аксіому застосовують у двох модифікаціях як аналог аксіоми мінімальної віддалі. Якщо метризовані матриці узгоджені, використовують аксіому 5а, а якщо ні – то аксіому 5b.

АКСІОМА 5а. Якщо відношення Р та Q відрізняються лише однією впорядкованою парою альтернатив (х_i, x_j), то віддаль між ними задано наступним співвідношенням:

де w – число, що задовольняє умову

тобто можна вибрати

АКСІОМА 5b. Якщо відношення Р та Q відрізняються лише однією впорядкованою парою альтернатив (х_i, x_j), то віддаль між ними становить

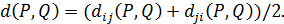
Виходячи з цих аксіом, доводиться, як і для розглянутих вище ранжувань, що система аксіом однозначно задає міру близькості на довільних адитивних метризованих відношеннях, а з огляду на варіанти аксіоми 5 можна вивести формули для обчислення відстані. Наведемо лише остаточні результати у вигляді таких теорем (схема доведення така сама, як раніше).

Теорема 3.4. Міра близькості між узгодженими адитивними метризованими відношеннями толерантності, еквівалентності, частково впорядкованими множинами, ранжуваннями, що задовольняють за аксіоми 1–4, 5а, визначається за формулою:

де

і значення w – деяке число, що задовольняє умову

тобто можна обрати

Теорема 3.5. Міра близькості для неузгоджених адитивних метризованих відношень, що задовольняють аксіоми 1–4, 5b, визначається за формулою

Приклад 3.12. У результаті експертного оцінювання отримано такі матриці відношень:

Знайдемо відстань між цими відношеннями. Оскільки задані відношення є узгодженими метризованими відношеннями порядку, то відстань між ними становить d (P ₁, Р ₂) = 50.

Приклад 3.13. Обчислимо відстань між визначеними двома експертами метризованими толерантностями, заданими матрицями:

Оскільки матриці узгоджені, то визначимо відстань між відношеннями Р ₁ і Р ₂ за формулами

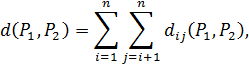
де

Приклад 3.14. Визначити відстань між двома відношеннями загального типу, заданими матрицями:

Оскільки відношення довільні, то

Інформацію про переваги можна подати також у вигляді вектора переваг , де n – кількість альтернатив, а кількість альтернатив, які переважають .

Якщо дані про переваги експерта подано як вектори переваг , то для виведення формули відстані між ними використовують аксіоми 1–4 й аксіому мінімальної віддалі 5с.

АКСІОМА 5с. Якщо вектори переваг та відрізняються лише однією і –ю компонентою, то відстань між ними становить

.

Тоді міру близькості між довільними векторами переваг та обчислюють за формулою

Приклад 3.15. Нехай два експерти надали для трьох альтернатив такі відношення:

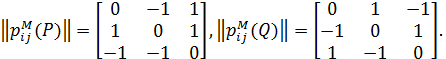
У першого експерта альтернативу х ₁ переважає одна альтернатива, х ₂ – жодної, х ₃ – дві. У другого експерта кожну з альтернатив переважає одна альтернатива. Тому вектори переваг становлять , а відстань між ними дорівнює 2.

Дата добавления: 2014-01-05