Структурні міри близькості

Використавши аналогію між мірами близькості на відношеннях і метриками на графах, можна отримати структурні міри близькості. Для цього розглянемо множину–носія відношень А = { х ₁, x ₂,..., x_n) і множину Р = { Р ₁, Р ₂,..., Р_n } усіх можливих відношень певного заданого типу з носієм А. Кожному відношенню Р_i Î Р поставимо у відповідність i –ту вершину скінченного графа G. Якщо два відношення Р_i, P_j Î Р сусідні, то їх з’єднано дугою. Кожній дузі графа поставимо у відповідність число, що характеризує віддаль між сусідніми відношеннями за певним законом, який відображає специфічні особливості міри. Уважатимемо, що відношення неметризовані, тому що в іншому випадку множина вершин графа G безмежна.

Поняття «знаходитися між» у цьому разі можна сформулювати так: уважаємо, що відношення Q знаходиться між відношеннями Р й R, якщо вершина графа G, що відповідає відношенню Q належить до найкоротшого шляху, що сполучає вершини, які відповідають відношенням Р й R. Якщо діють аксіоми 1–4 й 5d, то структурна міра близькості однозначна.

АКСІОМА 5d. Якщо Р й Q – сусідні відношення, то d (P, Q) = C_PQ – міра близькості між ними.

Отже, у загальному випадку, щоб визначити віддаль між довільними відношеннями, потрібно знайти в графі G найкоротший шлях між відповідними вершинами. Виходячи з того, що для n альтернатив і чи не найпростішого відношення строгого порядку кількість шляхів графа G становить n!, зрозуміло, що безпосереднє обчислення відстані практично неможливе. Тому використовують інший метод – конструктивно вводять структурні міри близькості.

Розглянемо випадок, коли для знаходження найкращих альтернатив використано ранжування. Природно вважати, що в ранжуваннях, які потрібно порівняти між собою, інверсії (перестановки) сусідніх альтернатив, що займають різні порядкові місця, нерівноцінні (інверсія на вищих місцях вагоміша, ніж на останніх). Тому для ранжувань відповідно змінюється аксіома 5d.

АКСІОМА 5е. Якщо ранжування Р та Q відрізняються лише інверсією альтернатив, що займають i –те й (і + 1)–ше місця, то d (P, Q) = c_i > 0, та с ₁ ³ с ₂ ³... ³ c_{n –1}, оскільки альтернативи ранжуються для виявлення найліпшої.

Якщо діють аксіоми 1–4, 5е, то структурна міра близькості на зважених (с ₁ ³ с ₂ ³... ³ c_{n –1}) ранжуваннях визначається за формулою

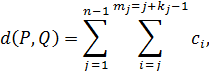
де k ³ 1 – кількість альтернатив, які водночас у ранжуванні Р гірші, ніж х_i, а в Q – кращі, ніж x_j. Це співвідношення задає у відповідному графі G довжину найкоротшого шляху між вершинами, що відповідають ранжуванням Р та Q.

Приклад 3.16. Нехай два експерти зазначили для п’яти альтернатив такі ранжування:

Р = { х ₂, x ₁, x ₄, х ₃, х ₅},

Q = { х ₄, x ₅, x ₃, х ₂, х ₁}.

Визначимо відстань між ними за структурною мірою близькості. Побудуємо таблицю, у яку зведемо результати обчислень.

Таблиця 3.2. Результати визначення структурної міри близькості

P	Q	Гірші	Кращі в	Ç	kj	j	mj	Сума
x 2	x 4	x 1; x 4; x 3	x 4; x 5; x 3	x 4; x 5; x 3				с 1+ с 2+ с 3
x 1	x 5	x 4; x 3; x 5	x 4; x 5; x 3; x 2	x 4; x 5; x 3				с 1+ с 2+ с 4
x 4	x 3	x 3; x 5	немає	немає				–
x 3	x 2	x 5	x 4; x 5	x 5				с 4
x 5	x 1	Немає	x 4	немає		–	–	–

Отже, віддаль становить

d (P, Q) = c ₁ + 2 с ₂ + 2 с ₃ + 2 с ₄.

Подібним способом уводять структурну міру близькості на еквівалентностях. У цьому випадку діють аксіоми 1, 2, 4 й 5f.

Структурні міри близькості на еквівалентностях можна задати по–різному. Ми розглянемо міру з такою властивістю: відстань між довільними відношеннями еквівалентності визначається найкоротшим шляхом між вершинами графа G, що відповідають еквівалентностям Р й R, який обов’язково проходить через вершину, котра відповідає еквівалентності .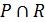

Відомо, що кожному відношенню еквівалентності відповідає розбиття елементів на класи еквівалентності, які ми позначатимемо так само, як і відповідне відношення еквівалентності, тому що з контексту зрозуміло, про що йдеться. Якщо Р та R – еквівалентності, то перетин 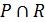еквівалентний такому розбиттю на класи, коли до одного класу 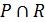нaлeжaтимуть елементи, що входять водночас до класу як у відношенні Р, так і в R. Отже, клас 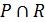складається з непорожніх перетинів класів еквівалентності Р та R.

Подрібненням розбиття Р буде таке розбиття R (позначимо P ® R), якщо для будь–якого класу еквівалентності R_i Î R знайдеться клас Р_j Î Р, такий що R_i Í Р_j. Очевидно, що Р ® 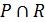та R ® 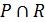. Нехай 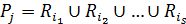. Позначимо як 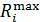той з класів еквівалентності 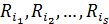, потужність якого найбільша (тобто до складу якого входить максимальна кількість елементів).

Поняття «між» визначається наступним чином – відношення еквівалентності Q знаходиться між відношеннями Р та R – [ Р, Q, R ], якщо 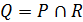; або Р ® R (R ® Р), і кожен клас еквівалентності з Q або має в собі один з класів 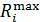, або входить в один з класів .

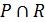Відношення еквівалентності Р та R називатимемо сусідніми, якщо Р ® R та Р відрізняється від R лише тим, що один з його класів еквівалентності замінений двома, тобто 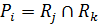, причому min{| R_j |, | R_k |} = 1. Таким чином конкретизуємо аксіому 5f.

АКСІОМА 5f. Якщо Р й R – сусідні відношення еквівалентності, то d (P, R) = 1.

Використавши аксіоми 1, 2, 4, 5f, можна довести, що значення структурної міри близькості між еквівалентностями Р й R визначається за формулою

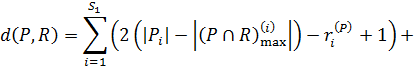
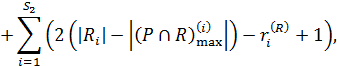
де S ₁, S ₂ – відповідно кількість класів у Р й R, 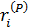та – відповідно кількість підкласів у Р_і й R_i.

Приклад 3.17. Задано два відношення еквівалентності у вигляді розбиття на класи:

Р = {(х ₁ ~ x ₂ ~ x ₃ ~ x ₄), (х ₅ ~ x ₆ ~ x ₇), (х ₈ ~ x ₉),(х ₁₀ ~ x ₁₁ ~ x ₁₂)}

R ={(х ₁ ~ x ₅ ~ x ₁₀), { х ₂ ~ x ₃ ~ x ₄ ~ x ₆~ x ₇), (х ₈ ~ x ₉), (х ₁₁), (х ₁₂)}

Потрібно обчислити відстань між ними за структурною мірою близькості.

Визначимо

Р Ç R = {(х ₁), (x ₂ ~ x ₃ ~ x ₄), (x ₅), (x ₆~ x ₇), (х ₈ ~ x ₉), (х ₁₀), (х ₁₁), (х ₁₂)},

S ₁ = 4, S ₂ = 5,

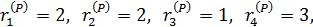
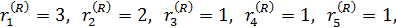
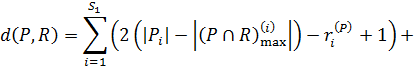
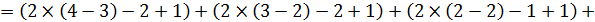
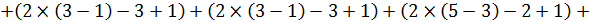
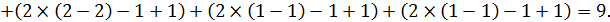
Дата добавления: 2014-01-05