Приклад 3.24. Порівняння проектів методом ранжування

Для складання стратегічного плану розвитку фірми було запропоновано вісім проектів як кандидати на включення. Позначимо їх А, В, С, D, Е, F, G, Н. Усі проекти проранжувала експертна комісія з 12 експертів (табл. 3.5). Ранг 1 експерти присвоювали найкращому проекту, який потрібно реалізувати, ранг 2 отримав другий за привабливістю проект і так далі, нарешті, ранг 8 – найсумнівніший проект, який варто реалізовувати лише в останню чергу.

Таблиця 3.5. Результати ранжування восьми проектів експертами

Номер експерта	А	В	С	D	Е	F	G	H
			2,5	2,5

Четвертий експерт уважає, що проекти С та D рівноцінні, й поступаються лише одному проекту – F. Тому вони мали б посісти друге та третє місця й одержати 2 та 3 бали. Оскільки проекти рівноцінні, то їх оцінено середнім балом (2+3)/2 = 5/2 = 2,5. Аналізуючи результати роботи експертів, зауважимо, що повної згоди між ними немає, а тому наведені в табл. 3.5 дані слід розглянути ретельніше.

На практиці найчастіше обчислюють середні арифметичні значення рангів проектів (табл. 3.6). За середніми рангами будують підсумкове ранжування, виходячи з такого принципу: що менше значення середнього рангу, то кращий проект. Найменший середній ранг (2,625) має проект D. Отже, у підсумковому ранжуванні він отримує ранг 1. Наступна сума (3,125) у проекту С, і він одержує підсумковий ранг 2. Проекти В й F мають однакові суми (3,25), тому з погляду експертів вони рівноцінні, тому мали б посісти місця 3 та 4. Ці проекти одержують середній бал (3+4)/2 = 3,5. Отже, підсумкове ранжування має вигляд

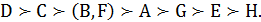
Проте ми неодноразово наголошували, що, оскільки оцінки експертів подано в порядковій шкалі, то усереднення за допомогою середнього арифметичного некоректне! У цьому разі слід обчислювати не середнє арифметичне, а медіану. Беремо ранги, що відповідають кожному з проектів (табл. 3.5). Наприклад, для проекту А це 5, 5, 1, 6, 8, 5, 6, 5, 6, 5, 7, 1. Розміщуємо їх у порядку неспадання (деякі відповіді можуть збігатися, тому порядок саме такий). Для проекту А отримаємо послідовність 1, 1, 5, 5, 5, 5, 5, 6, 6, 6, 7, 8. У ній на центральних місцях – шостому та сьомому – 5 і 5. Отже, значення медіани – 5.

Таблиця 3.6. Результати обчислення середніх арифметичних і медіан

Проект	А	В	С	D	Е	F	G	Н
Сума рангів			37,5	31,5
Середнє арифметичне рангів		3,25	3,125	2,625	6,333	3,25	5,333	7,083
Підсумковий ранг за середнім арифметичним		3,5				3,5
Медіана рангів				2,25	7,5
Підсумковий ранг за медіанами		2,5	2,5

Обчислені значення медіан проектів наведено в передостанньому рядку табл. 3.6. Тут медіани визначено за звичайними правилами статистики — як середнє арифметичне центральних компонент варіаційного ряду. Підсумкове впорядкування проектів за значеннями медіан наведено в останньому рядку табл. 3.6. Ранжування за медіанами має вигляд

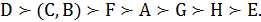
Оскільки проекти С та В мають однакові значення медіан рангів, то за цим методом ранжування вони еквівалентні, тому їх об’єднано в групу (кластер).

Порівняння одержаних ранжувань показує їх схожість. Є лише одна істотна розбіжність, що стосується впорядкування проектів Н і Е. Проте ці проекти найменш привабливі серед розглянутих, тому обираючи проекти для подальшого обговорення та використання, можна не зважати на цю розбіжність.

Метод гіперупорядкування дає змогу отримати більше інформації про переваги альтернатив, аніж попередні. У ньому в експерта має бути можливість ранжувати різниці оцінок альтернатив, щоб мати додаткову інформацію про співвідношення між їх числовими оцінками. Спочатку експерт ранжує альтернативи, а на наступному етапі — різниці оцінок для сусідніх ранжувань. Для ранжування різниць оцінок альтернатив застосовують ті самі методи, що й для ранжування альтернатив.

Приклад 3.25. Експерт має оцінити переваги на множині з чотирьох альтернатив A = { x ₁, х ₂, х ₃, х ₄}. Після ранжування одержано такий лінійний порядок:

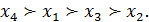
Цьому ранжуванню можуть відповідати, наприклад, такі варіанти розміщення альтернатив на числовій осі:

На наступному етапі гіперупорядкування експерт ранжує різниці оцінок сусідніх в отриманому ранжуванні за перевагою альтернатив, тобто

{ f (x ₄) – f (x ₁); f (x ₁) – f (x ₃); f (x ₃) – f (x ₂)}.

Результатом цього етапу — ранжування

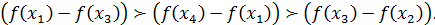
Порівнюючи з можливими варіантами а – d, упевнюємося, що гіперпорядку, який оцінив експерт, відповідають варіанти b та с. Справді, гіперупорядкування інформативніше, ніж звичайне ранжування.

Метод векторів переваг дає змогу достатньо просто одержати інформацію про порівняльну важливість альтернатив: для кожної альтернативи х_i Î А експерт має зазначити, скільки альтернатив із множини А = { х ₁,..., х_n } переважають її (тобто зазначають лише кількість таких альтернатив, а не самі альтернативи). Експерт може зазначити й кількість альтернатив, гірших за розглянуту. Отримаємо вектор z = { z ₁,..., z_n }, де z_i — відносна перевага альтернативи х_i. За допомогою вектора переваг можна подати інформацію про результати попарних та множинних порівнянь, а також ранжувань.

Проте обернене твердження не виконується, і можна лише ставити задачу про знаходження відношення певного типу (наприклад, ранжування), яке згідно з визначеною метрикою «найближче» до одержаного вектора переваг.

Виконуючи класифікацію альтернатив, можна застосовувати ті самі стратегії дій, що й у методі попарних порівнянь або ранжування. Якщо ж є додаткова кількісна інформація, то доцільно використовувати алгоритми та методи кластерного аналізу.

Отже, ми розглянули методи отримання якісних оцінок і далі проаналізуємо методи одержання кількісних оцінок від експерта.

Дата добавления: 2014-01-05