Методи отримання кількісних експертних оцінок

Метод безпосередньо числового оцінювання альтернатив полягає у визначенні експертом для кожної альтернативи х_i Î А числа f (х_i), що задає її важливість. Якщо такі оцінки відомі, то (за умови застосовності певного типу шкали вимірювань!) можна визначити, наскільки чи в скільки разів одна альтернатива переважає іншу. Крім того, ми вважаємо, що всі альтернативи порівнянні між собою, і не виникає випадків нетранзитивності.

Достатньо часто, щоб вимірювання всіх експертів були порівнянними, для безпосереднього оцінювання використовують шкалу в балах (наприклад, щоб оцінювати знання школярів і студентів). Якщо альтернатив достатньо багато, для безпосереднього оцінювання застосовують метод середньої точки: експерт спочатку зазначає «найгіршу» (х ₁) і «найкращу» (х ₂) альтернативи, потім йому пропонують зазначити «середню» альтернативу (х ₃), для якої

f (х ₃) = (f (х ₁) + f (х ₂))/2,

і процес поділу триває до моменту розміщення всіх альтернатив на числовій осі.

Для числового оцінювання якості альтернатив достатньо часто застосовують метод Черчмена —Акоффа, що ґрунтується на таких припущеннях.

v Кожній альтернативі х_i можна поставити у відповідність число f (х_i) £ 0.

v Якщо альтернатива х_i переважає х_j, то f (х_i) > f (х_j).

v Якщо альтернатива х_i й х_j рівноцінні, то f (х_i) = f (х_j).

v Якщо числа f (х_i) та f (х_j) відображають якість альтернатив х_i й х_j, то f (х_i) + f (х_j) відповідає якості сумісної реалізації альтернатив х_i й х_j (це найсильніша з наведених умов – умова адитивності альтернатив, — яка в більшості випадків не виконується).

Спочатку альтернативи ранжуються за важливістю (будемо вважати, що х ₁,..., х_n вже проранжовані в порядку індексування, тобто 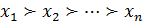. Експерт вказує попередні числові оцінки f (х ₁),..., f (х_n) (інколи найкраща альтернатива отримує оцінку 1, а оцінки всіх інших коливаються в межах від 0 до 1). Надалі експерт порівнює х ₁ та сумарну дію альтернатив х ₂,..., х_n. Якщо х ₁ важливіша за цю суму, експерт корегує оцінки, так щоб виконувалось співвідношення

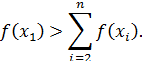
У протилежному випадку має виконуватись нерівність

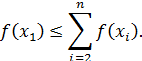
Якщо виникає така ситуація, тобто альтернатива х ₁ менш важлива, ніж сума всіх альтернатив, що залишилися, для уточнення її послідовно порівнюють із сумами

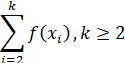
у порядку зменшення значення k від n – 1 до 2. Як тільки знайдено перше k, для якого виконується умова

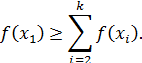
альтернативу х ₁ виключають із розгляду. Потім аналогічно корегують значення числових оцінок для наступних альтернатив. Коли альтернатив багато, для зменшення трудомісткості методу їх розбивають на групи, включивши одну з них до складу всіх груп, щоб отримати числові оцінки для всіх альтернатив за допомогою оцінювання всередині кожної групи. Метод Черчмена — Акоффа можна застосовувати й у разі вимірювання в шкалі відношень. У цьому випадку експерт зазначає, у скільки разів альтернативи важливі менше за найважливішу.

Розглянемо межі коректності застосування методу Черчмена — Акоффа, тобто визначемо, при вимірюванні в яких шкалах, операції що використовуються в ньому, є коректними. Припустімо, що порівнюються числові характеристики двох сукупностей альтернатив, і

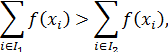
де I ₁, І ₂ – множини індексів альтернатив, 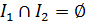, числові характеристики виміряно в шкалі інтервалів. Будемо вважати, що I ₁ = {1}, І ₂ = {2, 3}, тобто f (х ₁) > f (x ₂) + f (x ₃). Якщо переваги виміряно в шкалі інтервалів, то af (х ₁) + b > af (х ₂) + af (х ₃)+ 2 b, тобто для конкретних числових оцінок альтернатив можна вказати такі значення, за яких нерівність порушиться. Отже, перетворення, що виконуються в методі Черчмена – Акоффа, некоректні в разі вимірювань у шкалі інтервалів. Для вимірювань у шкалі відношень

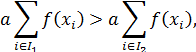
тобто метод коректний.

У методі Терстоуна первинною інформацією для визначення числових оцінок альтернатив є результати попарних порівнянь, а оцінка кожної альтернативи є випадковою величиною. Вважаємо, що вона розподілена за нормальним законом із математичним сподіванням М_i та дисперсією D_i, а її реалізацію оцінює експерт. Різниця оцінок – випадкових величин f (х_i) та f (x_j) – також розподілена за нормальним законом із математичним сподіванням і дисперсією

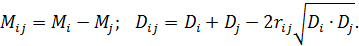
де 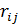– коефіцієнт кореляції між f (х_i) та f (x_j).

Результатом застосування методу є значення M_i, і Î {1, 2, …, n }, які обираються як числові оцінки альтернатив за значеннями частот S_ij. Тут S_ij – частота вибору альтернативи х_i як важливішої порівняно з х_j,

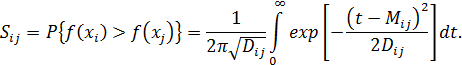
Визначивши за допомогою таблиці квантилів нормального розподілу відношення 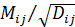, одержимо 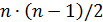рівнянь

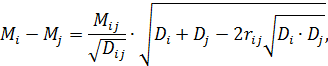
у яких невідомих більше, ніж змінних.

Далі робимо додаткові припущення про те, що кореляція відсутня, а середньоквадратичні відхилення рівні між собою: 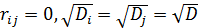. Отримаємо систему рівнянь

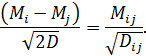
Нарешті, узявши за одиницю шкали вимірювання значення 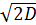, одержимо остаточну систему рівнянь

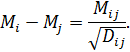
Якщо вона несумісна, то розв’язок можна знайти методом найменших квадратів, отримавши остаточні значення М_i.

Метод фон Ноймана–Морґенштерна також виходить зі стохастичного характеру значень оцінок. У ньому для визначення оцінок використано суміші ймовірностей. Вважається, що експерт може вказати для довільної альтернативи х_j, гіршої за х_i, але кращої, ніж х_l таке число р, (0 £ р £ 1), що альтернатива х_j буде еквівалентна «мішаній» альтернативі 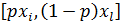. Цю альтернативу можна реалізувати за допомогою стохастичного вибору, коли альтернативу х_i обирають з імовірністю р, а х_l – з імовірністю (1 – р). Якщо ймовірність р досить близька до 1, то

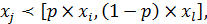
а коли вона близька до 0, то

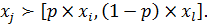
Окрім того, вважаємо, що діють аксіоми зв’язності та транзитивності відношення переваг, і якщо р > р’, то для двох мішаних альтернатив завжди виконується співвідношення

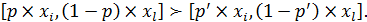
Якщо виконується певна система аксіом, то для кожної з основних альтернатив х ₁, …, x_n задано числа u ₁, …, u_n, що характеризують числову оцінку мішаних (і як частковий випадок – не мішаних) альтернатив. Це означає, що існує певна функція корисності u ₁ p ₁ + u ₂ p ₂ + … + u_np_n, і найкращою є альтернатива, для якої значення функції корисності найбільше.

Отже, оцінювати альтернативи у вигляді одного числа слід обережно, розуміючи, що для достатньо складних альтернатив таке оцінювання суттєво недостатнє. У практичному застосуванні методу необхідно враховувати обмеження, які накладаються методами отримання відповідної експертної інформації. Водночас для попередньої орієнтовної оцінки альтернатив доцільно застосовувати методи числового оцінювання.

Дата добавления: 2014-01-05