Прості мережі Петрі

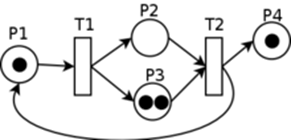
Мережа Петрі є орієнтованим дводольним графом, який має чотири базових елементи (рис. 3.2):

v вузли, або місця (places);

v переходи (transitions);

v дуги (arcs);

v маркери (tokens).

Рис. 3.2. Приклад мережі Петрі: білими кружками позначені вузли, смужками - переходи, чорними кружками - маркери	Рис. 3.3.Приклад дводольного графу

Дводольний граф – це граф, множину вузлів якого можна розбити на дві частини таким чином, що кожне ребро графа сполучає якийсь вузол з однієї частини з якимсь вузлом іншої частини, тобто не існує ребра, що сполучає два вузли з однієї і тієї ж частини (рис. 3.3).

Вузли позначаються кружками і визначають стан, в якому може знаходитись мережа або її частина.

Переходи – це активні елементи мережі, які позначають дії, виконувані під час спрацювання переходів. Для того щоб перехід міг спрацювати, необхідне виконання певних умов, які визначаються наявністю маркерів у вузлах мережі, з'єднаних з переходом. Якщо умови настання подій виконано, то вважають, що перехід збуджений. Переходи позначаються короткими вертикальними або горизонтальними лініями.

Вузли та переходи з'єднуються орієнтованими ребрами (дугами). Вузли, з яких виходять дуги до певного переходу, називаються вхідними вузлами переходу, а вузли, до яких ведуть дуги з певного переходу, – вихідними. Два вузли або два переходи з'єднуватись дугами не можуть. Кожний перехід може бути з'єднаним з вузлом тільки однією дугою (вхідною або вихідною).

Функціонування мережі Петрі можна описати різними способами. Наприклад, можна розглядати вузли як певні умови, а переходи — як події. Таким чином, стан мережі в кожний момент часу задається системою умов. Для зручності задания умов у мережі Петрі вводяться маркери (фішки), які зображуються крапками всередині вузлів. Виникнення певної комбінації маркерів у вузлах приводить до настання деякої події, яка у свою чергу викликає зміну стану умов мережі. Стан маркування або стан мережі Петрі визначається сукупністю маркерів кожного окремого вузла мережі.

На рис. 3.4 зліва зображено просту мережу Петрі з одним переходом, трьома вузлами, два з яких містять маркери. Перехід, в якого всі вхідні вузли містять маркери, називається збудженим. Збуджений перехід може спрацювати, після чого всі маркери із вхідних вузлів переходу перемістяться у вихідні. Таким чином, настає подія, яка змінює стан мережі.

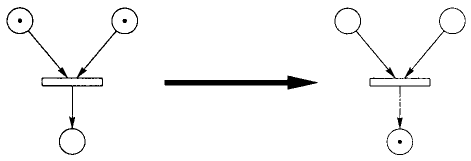
Рис. 3.4. Проста мережа Петрі та графічне зображення спрацювання переходу

Якщо одночасно збуджуються кілька переходів мережі, виникає невизначеність, тому одночасне спрацювання кількох переходів у мережі Петрі неможливе, тобто переходи спрацьовують послідовно, миттєво. Незважаючи на те, що маркери змінюють своє положення у вузлах, прості мережі Петрі – це статичні моделі, в яких не враховується динаміка в часі (зміна станів мережі не залежить від моментів часу).

Для того щоб за допомогою мережі Петрі відтворити динаміку роботи деякої детермінованої динамічної системи в часі, необхідно зазначати моменти спрацьовування переходів. Такі можливості мають тільки розширення мереж Петрі, в яких спрацювання переходів здійснюється в задані моменти модельного часу з деяким постійним кроком D t.

цветная сеть — маркеры могут быть различных типов, обозначаемых цветами, тип маркера может быть использован как аргумент в функциональных сетях;

иерархическая сеть — содержит не мгновенные переходы, в которые вложены другие, возможно, также иерархические, сети. Срабатывание такого перехода характеризует выполнение полного жизненного цикла вложенной сети.

До основних видів мереж Петрі відносяться наступні:

v тимчасова мережа – переходи володіють вагою, що визначає тривалість спрацьовування (затримку);

v стохастична мережа – затримки є випадковими величинами;

v функціональна мережа – затримки визначаються як функції деяких аргументів, наприклад, кількості маркерів в якись вузлах, стану деяких переходів;

v кольорова мережа – маркери можуть бути різних типів, що означають кольорами, тип маркера може бути використаний як аргумент у функціональних мережах;

v ієрархічна мережа – містить не миттєві переходи, в які вкладені інші, можливо, також ієрархічні, мережі. Спрацьовування такого переходу характеризує виконання повного життєвого циклу вкладеної мережі.

Основними властивостями мережі Петрі є:

v обмеженість – число маркерів у будь-якому вузлі мережі не може перевищити деякого значення K;

v безпека – окремий випадок обмеженості, K = 1;

v зберігатимисть – постійність завантаження ресурсів (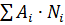постійна, де 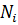– число маркерів в i -му вузлі, 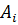– ваговий коефіцієнт);

v досяжність – можливість переходу мережі з одного заданого стану (що характеризується розподілом маркерів) в інше;

v жвавість – можливість спрацьовування будь-якого переходу при функціонуванні модельованого об'єкту.

Дата добавления: 2014-01-05