Розмітка мережі Петрі

Розмітка М мережі Петрі — це функція, яка ставить у відповідність маркерам вузлів цілі додатні числа. Суть розмітки полягає в приписуванні кожному вузлу певної кількості маркерів. Наприклад, якщо позначити через N саму мережу Петрі, через Р — множину вузлів у мережі N, через n (Р) — кількість вузлів, то кожному вузлу цієї мережі можна поставити у відповідність число із послідовності {1, 2, …, n (Р)}. Таким чином, розмітку М можна зобразити за допомогою вектора з n (Р) елементів, в якому і -й елемент визначає кількість маркерів у і -му вузлі. У загальному випадку кількість маркерів у вузлі може бути більшою за одиницю.

На рис. 3.5 зображено мережу Петрі, яка може перейти в такий стан, коли жоден з переходів не буде збудженим. Мережа в такому стані називається заблокованою. Розмітка заблокованої мережі задається такими елементами:

v М = [2, 0, 0] – кількість маркерів у вузлах;

v Р = {1, 2, 3} – вузли мережі;

v n (Р) = 3 – кількість вузлів в мережі;

v a, b, c, d – переходи.

Переходи a, b можуть бути збудженими, а переходи с, d — ні. У результаті збудження та спрацьовування переходу а отримуємо розмітку М ¹ = [1, 1, 0], за якої збуджуються переходи а, b і с. У разі спрацювання переходу с отримуємо мережу з новою розміткою М ² = [2, 0, 0]. У мережах Петрі паралельне спрацювання переходів обмежується тільки кількістю маркерів у вузлах, тобто для спрацьовування переходів мають бути маркери у всіх вхідних вузлах.

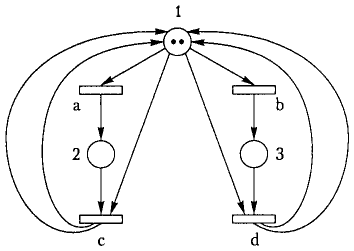
Рис. 3.5. Мережа Петрі, яка може бути заблокованою

При початковій розмітці мережі, яку зображено на рис. 3.5, переходи а і b можуть збуджуватись одночасно. Однак збудження двох переходів в один і той же момент часу не означає, що вони можуть одночасно спрацьовувати. Наприклад, переходи а та b мережі з розміткою М = [1, 0, 0] можуть одночасно тільки збуджуватись, але не спрацьовувати. Причина в тому, що в разі спрацювання як переходу а, так і переходу b повинні одночасно зникнути обидва маркери з першого вузла, що неможливо.

Перехід, в якого немає жодного вхідного вузла, завжди є збудженим і може видавати (генерувати) маркери. Генерування маркерів можна розглядати як послідовне виконання функції розмітки М, тобто послідовність зміни розміток M ⁰, M ¹, M ²,..., де М^{i +1} отримане із Мⁱ у результаті збудження деякого переходу. Тут М ⁰ — початкова розмітка мережі Петрі.

Перехід, який не має жодної вихідної дуги і має тільки одну вхідну дугу, збуджений завжди тільки в тому випадку, якщо вхідний вузол містить маркер. Такий перехід може знищувати маркери.

У загальному випадку для заданої мережі N з початковою розміткою М ⁰ є багато можливих послідовностей спрацювання переходів. Мережа Петрі знаходиться в «живому» стані (живуча розмітка), коли кожний з переходів може збуджуватись нескінченну кількість разів.

Мережа Петрі знаходиться в «мертвому» стані (заблокована), якщо вона не має жодного збудженого переходу. Заблокована мережа є стійкою, тобто її маркери не можуть змінювати свої позиції у вузлах. На рис. 3.5 зображено мережу з початковою розміткою М ⁰ = [2, 0, 0]. У разі спрацювання переходів а і b початкова розмітка замінюється на розмітку М ² = [0, 1, 1]. Мережа з такою розміткою стане заблокованою, і жодний з переходів не зможе бути збудженим. Отже, розмітка М ⁰ не є живучою. Дійсно, для цієї мережі не існує живучих розміток. Незалежно від кількості маркерів у вузлі 1 переходи а і b будуть спрацьовувати доти, доки всі маркери не перейдуть у вузли 2, 3. Коли у вузлі 1 не залишиться маркерів, мережа заблокується.

Вважають, що два переходи конфліктують, якщо вони не можуть бути збудженими одночасно. Незважаючи на те, що умови конфлікту формально точно не визначені, зрозуміло, що суть конфлікту тісно пов'язана з типом тупикової ситуації, яка мала місце в мережі, зображеній на рис. 3.5, де переходи с і d конфліктують при розмітці М ⁰.

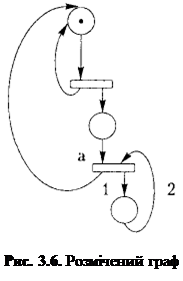
Теорем, якими задаються умови блокування та скінченності мереж Петрі, не існує. Подібні теореми доведено тільки для розмічених графів, які є простішими за мережі Петрі. Для графів тільки певних типів доведено, що перехід, який не може бути збудженим, існує лише в тому випадку, якщо в графі існує орієнтований цикл без маркерів. Для мереж Петрі аналогічного твердження довести не вдалось. У розміченому графі, зображеному на рис. 3.6, перехід а мертвий, оскільки дуги 1 і 2 створюють орієнтований цикл, який не має маркерів.

Дата добавления: 2014-01-05