Формальне визначення мереж Петрі

Існує кілька способів формального опису мереж Петрі, які відрізняються способами задания елементів і зв'язків. Згідно з працею [26] будемо визначати мережу Петрі трьома елементами:

,

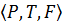дe P – непорожня множина елементів мережі, названих вузлами;

Т – непорожня множина елементів мережі, названих переходами;

F – функція інцидентності, що задає зв'язок між елементами множин Р і Т.

Для мережі Петрі, визначеної елементами 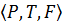, повинні виконуватись такі умови.

1. 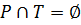, тобто множини вузлів і переходів не перетинаються.

2. 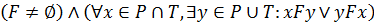, тобто будь-який елемент мережі інцидентний хоча б одному елементу іншого типу.

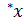3. Якщо для довільного елемента мережі позначити через множину його вхідних елементів, а через 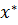— множину його вихідних елементів, то

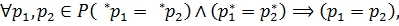
тобто мережа не міститиме пари вузлів, які інциденти до тієї ж множини переходів.

На основі поняття мережі Петрі, яка описує тільки статичну топологію модельованого процесу або системи, вводяться динамічні мережні структури, в яких вузлам приписуються спеціальні розмітки для моделювання виконання умов. З мережею пов'язують поняття її функціонування, яке описується зміною її розмітки (умови) у результаті спрацювання переходів. До динамічних мереж відносяться мережі Петрі та їх різні узагальнені варіанти. Таким чином, мережа Петрі не є динамічною системою, в якій стан моделі змінюється в часі, він змінюється тільки в разі спрацювання переходів і зміни розмітки.

Зміну позицій маркерів у вузлах можна визначити, якщо задати мережу Петрі як структуру 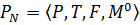, де 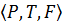— скінченна мережа (множини Р і T скінченні), а М ⁰ — початкова розмітка мережі, яка ставить у відповідність будь-якому вузлу р_i Î Р деяке число М ⁰(р) = n.

Функціонування мережі Петрі описується за допомогою множини послідовностей спрацьовувань і множини досяжних у мережі розміток. Ці поняття визначаються через правила спрацювання переходів мережі.

Розмітка мережі P_N є функцією М: P Þ N (N — множина натуральних чисел). Якщо припустити, що всі вузли мережі строго впорядковані деяким чином, тобто Р = (p ₁, p ₂, …, p_n), то розмітку М мережі (у тому числі і початкову розмітку) можна задати як вектор чисел М = [ m ₁, m ₂, …, m_n ] такий, що для будь-якого i (1 £ і £ n) m_i = М (p_і). Якщо Р' = (p_{i 1}, p_{і 2},..., p_ik) – підмножина вузлів з Р, то умовимося через М (Р') позначати множину розміток { М (p_{i 1}),..., M(p_ik)}. Якщо Р' представити як вектор Р' = (p_{i 1}, p_{і 2},..., p_ik), то М (Р') позначає вектор проекцїї розмітки М на Р'.

Перехід t Î Т може спрацювати при деякій розмітці М мережі Р, якщо 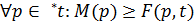, тобто кожний вхідний вузол р переходу t має розмітку, не меншу, ніж кратність дуги, що з'єднує р і t. Цю умову можна записати як .

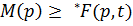Для ординарної мережі Петрі (тобто мережі, в якій дуги мають кратність, рівну 1) умова спрацьовування переходу означає, що будь-який вхідний вузол цього переходу містить хоча б один маркер, тобто має ненульову розмітку.

Спрацьовування переходу t розміткою М породжує розмітку М' за таким правилом:

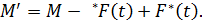
На множині розміток уводять відношення [> безпосереднього проходження розміток:

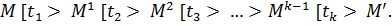
Слово t у цьому випадку називається послідовністю перемикань, які ведуть від М до М'.

Множину розміток, досяжних у мережі P_N від розмітки М, позначимо через R (P_N, М). Якщо R (P_N) = R (P_N, М ⁰), то множину всіх розміток, досяжних у мережі P_N від початкової розмітки М ⁰, називають множиною досяжних розміток мережі. Властивості мережі Петрі визначають, досліджуючи можливі послідовності спрацьовувань переходів і множини досяжних у мережі розміток.

Дата добавления: 2014-01-05