Розширення можливостей дуг під час моделювання

Зміни стану мережі Петрі, тобто переміщення маркерів, спричинені діями переходів, у разі спрацювання яких маркери вилучаються із одних вузлів і поміщаються в інші; таким чином формуються потоки даних. Способи вилучення і розміщення маркерів визначаються спрямованими дугами, які з'єднують вузли та переходи. У системах моделювання з кожною дугою можна пов'язати не тільки певний ваговий коефіцієнт (вагу), а й будь-яку функцію, що визначається як вираз дуги. У загальному випадку вираз дуги — це функція або значення (числове, символьне і т. ін.), згідно з яким збуджується перехід і змінюється положення маркера під час моделювання.

Якщо під час моделювання значення виразу дуги не змінюється, то для спрацювання переходу необхідна наявність у вузлі маркера, який співпадав би із значенням виразу дуги (рис. 3.13).

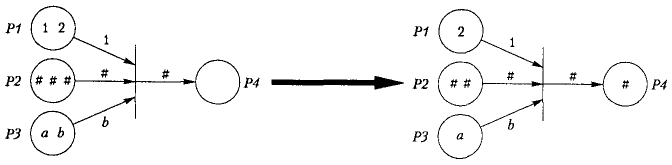
Рис. 3.13. Дуги з постійними виразами

Наприклад, лівий перехід, зображений на рис. 3.13, спрацьовує тільки за умови, що у вузлі Р 1 знаходиться хоча б один маркер 1, у вузлі Р 2 – хоча б один маркер # (у системі моделювання POSES++ символом # позначається чорний маркер) і у вузлі Р 3 – один маркер типу b. Після спрацювання переходу зазначені маркери вилучаються із вузлів Р 1, Р 2 та Р 3, а у вузол Р 4 поміщається маркер #.

Дуги, вираз яких не є константою, найчастіше використовуються для моделювання фіксованих потоків даних. Дуги зі змінними виразами застосовуються в тих випадках, коли заздалегідь неможливо задати значення параметрів моделі, наприклад під час пошуку даних і перевірки деяких умов, що змінюються в процесі моделювання. Вираз дуги такого типу називається змінною відповідності. Змінні відповідності — це дані особливого типу, і їм не можна присвоїти значення явно, як звичайним змінним. Свої значення вони можуть отримувати тільки в разі збудження переходів.

На рис. 3.14 видно, що змінна х є значенням виразу дуги, яка з'єднує вузол Р 1 і перехід Т 1. Оскільки для вузла заданий режим FIFORAM і маркер 1 є першим у черзі вузла Р 1, то змінній відповідності х присвоюється значення 1. Це ж значення присвоюється і виразу дуги, яка з'єднує перехід з вузлом Р 2, для якого теж встановлений режим FIFORAM. Для вузла Р 3 задано режим FIFO, тому змінній у присвоюється значення а. Таким чином, після спрацювання переходу у вузлі Р 4 знаходяться маркери 1 та а.

Правило спрацювання переходу можна описати також таким чином. У вузлі Р 1 знайти перший маркер і присвоїти його значення змінній відповідності х, тобто х = 1. Потім у вузлі Р 2 знайти маркер із значенням, ідентичним х = 1. Після цього у вузлі Р 3 знайти перший маркер у черзі (у даному випадку маркер а) і присвоїти його значення змінній відповідності у, тобто у = а. Після спрацювання переходу у вузлах Р 1 і Р 2 знищити маркер 1, а у вузлі Р 3 — маркер а. Згенерувати у вузлі Р 4 маркери, які складаються з комбінації значень (х, у).

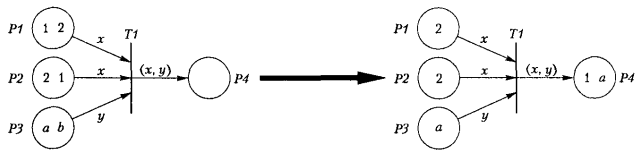
Рис. 3.12. Дуги з використанням змінних відповідності

Якщо для переходу не задане обмеження стосовно кількості паралельних спрацювань, то перехід зразу ж може спрацювати повторно. У цьому випадку перевіряються маркери, які залишились у вхідних вузлах переходу, тобто маркери 2 та b. Ці значення присвоюються змінним відповідності дуг. У цьому разі значення х, які використовувались під час попереднього спрацювання, не враховуються.

Застосування змінних відповідності пов'язане з послідовністю перегляду вхідних дуг переходу. Якби в наведеному вище прикладі першою вхідною дугою переходу Т 1 була дуга, що йде від переходу Р 2, а не від Р 1, то після спрацювання переходу у вузлі Р 4 знаходились би маркери 2 і b.

Покажемо, яким чином можна спростити мережу Петрі, використовуючи вирази для дуг.

Дата добавления: 2014-01-05