Приклад 3.3

Розглянемо ще один приклад — проблему філософів, що обідають, відому з літературних джерел як задачу Эдсгера В.Дейкстри. Це класичний приклад задачі, яку часто використовують для пояснення паралельних процесів і пов'язаних з ними умов блокування, чи взаємовиключення («зависання»), або для пояснення стратегії використання глобального ресурсу в моделях. Одночасно приклад ілюструє, наскільки важкі іноді для розуміння процеси, які виникають у дуже простих паралельних структурах.

За одним круглим столом (рис. 3.15) сидять п'ять філософів. Перед кожним із них стоїть тарілка з їжею, а між тарілками лежать палички для їжі (всього п'ять паличок). Деякий час кожний філософ зайнятий роздумами, а як зголодніє, він починає втамовувати голод. Для їжі кожному філософу потрібно взяти дві палички — спочатку ту, що зліва, а потім ту, що справа. Втамувавши голод, філософ кладе палички на місце і знову переходить до роздумів. Цей процес може тривати досить довго. Щоб поїсти, філософи конкурують між собою за палички для їжі, і, таким чином, палички для їжі є глобальним ресурсом у системі.

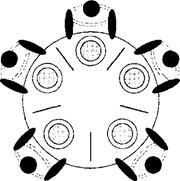
Рис. 3.15. Ілюстрація проблеми філософів, що обідають

Завдання полягає в тому, щоб побудувати таку модель, яка дала б змогу синхронізувати дії всіх філософів таким чином, щоб не виникло взаємного блокування моделі. Блокування може виникнути тоді, коли всі філософи сядуть за стіл і кожен з них намагатиметься одночасно взяти дві палички. У цьому разі виникає ситуація, коли кожен із філософів візьме лише одну паличку, і таким чином, жоден з них не зможе їсти. Такий розподіл глобального ресурсу називається зависанням мережі.

Під час побудови моделі слід ураховувати той важливий факт, що філософ повинен брати спочатку ліву паличку, а потім праву. Обидві палички брати одночасно заборонено. Неузгоджений доступ до паличок визначає критичний процес, який має бути глобально синхронізованим таким чином, щоб уникати конфліктів між філософами, наприклад у випадку, коли два філософи одночасно намагаються взяти одну й ту ж паличку.

Для формалізації моделі за допомогою мережі Петрі спочатку потрібно визначити об'єкти моделі і задати для них структури даних. Об'єктами моделі є п'ять філософів і п'ять паличок для їжі. Для кожного філософа необхідно визначити, які палички для їжі знаходяться зліва й справа від нього. Це можна легко зробити, якщо присвоїти номери філософам і паличкам (від 0 до 4). Паличці, яка лежить зліва від філософа, слід присвоїти той же номер, що й філософу, а паличці справа — на одиницю більший. Виняток буде зроблено тільки для четвертого філософа. Зліва від нього буде розташована паличка під номером 4, а справа — під номером 0. Таким чином, нумерацію паличок можна записати як

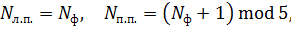
де 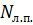, , 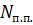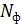— номери лівої, правої палички та філософа відповідно.

Очевидно, що одночасно можуть їсти тільки два філософи, тому що п'яти паличок для їжі вистачить тільки для двох.

Далі треба визначити стани об'єктів. Філософ може бути зайнятий роздумами або їжею. Ці можливі стани філософів позначимо як роздуми та їжа. Позначимо також можливі стани паличок як вільна і зайнята. Палички для їжі вважаються зайнятими, якщо філософ знаходиться в стані їжа. На початку моделювання всі філософи знаходились у стані роздуми, а палички для їжі — у стані вільна.

Після того, як визначено всі об'єкти моделі та їх можливі стани, можна задати процеси і дії, які будуть виконувати ці об'єкти (рис. 3.16).

Процес взяти:

v філософ бере спочатку ліву, а потім праву паличку.

Процес покласти:

v філософ кладе обидві палички на місце.

Щоб запобігти блокуванню моделі, кожний філософ повинен переходити від стану роздумів до їжі й навпаки в довільні моменти часу. Отже, для вузлів роздуми і їжа необхідно встановити режим доступу RAM.

Синхронізація доступу до паличок (єдиного глобального ресурсу системи), так само як і розв'язання проблеми блокування моделі, здійснюється автоматично під час перевірок правил дуг для спрацювання переходів. Незалежно від того, виконуються чи ні правила спрацювання переходів, модель ніколи не заблокується.

Отже, дії філософів можна описати такими правилами, номери яких позначено в дужках:

Процес взяти:

v якщо паличка, номер якої збігається з номером філософа, перебуває в стані вільна (1),

v паличка поряд з філософом, номер якої обчислюється як 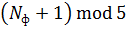, теж перебуває в стані вільна (2)

v і відповідний філософ з номером знаходиться в стані роздуми (3),

v то дві палички для їжі, що знаходяться справа і зліва від філософа, позначити як такі, що знаходяться в стані зайняті (1), (2),

v і позначити філософа як такого, що перейшов від стану роздуми до стану їжа (3), (4).

Процес покласти:

v якщо філософ з певним номером перебуває в стані їжа (5),

v змінити його стан від їжа до роздуми (5), (6)

v і палички для їжі, номери яких збігаються з номером філософа та з номером, що обчислюється за формулою 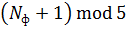, перевести в стан вільна (7), (8)

За допомогою наведених правил можна сформулювати вирази дуг у моделі мережі Петрі. На рис. 3.16 зображено мережу Петрі для цієї моделі.

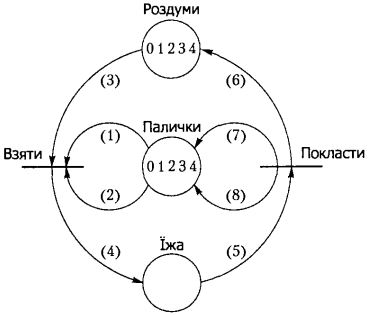
Рис. 3.16. Застосування мережі Петрі для вирішення проблеми філософів, що обідають

Незважаючи на складність такої проблеми, модель досить проста, і перетворення її у програму для моделювання доволі формальне.

Дата добавления: 2014-01-05