Точки доступа в цветной сети

S-точка доступа. Как видно из определения s-точки доступа, она задаётся множеством маркировок, которые считаются эквивалентными в смысле наступления состояний, определённых этими маркировками, в синхронизируемых по s-точке доступа сетях. При задании s-точки доступа в цветной сети, маркировки могут содержать в себе места, в которые могут поступать токены различных типов. Такие места при преобразовании в простую сеть разбиваются на множество мест, количество которых равно мощности множества значений токенов допустимых в этом месте. Согласно смыслу операции мы обязаны будем в синхронизированной сети раздробить эти места, чтобы удовлетворить множеству значений токенов во второй сети. Получается, что при синхронизации мест одинакового типа (с одинаковыми допустимыми типами токенов) значение параметров одной сети никак не влияет на значение параметров другой, то есть смысл операции в цветных и простых сетях может пониматься по-разному. Чтобы этого избежать, надо доопределить s-точку доступа:

Определение:

Пусть заданы: цветная сеть N и С – множество типов токенов в этой сети. Тогда s-точкой доступа сети N называется набор 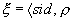, где

1. - имя (идентификатор) s-точки доступа;

2. 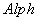- некоторый алфавит;

3. - множество такое, что .

4. 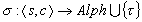, где 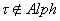, причём если 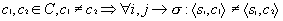. - пометочная функция мест, ставящая в соответствие каждому типу токена в месте уникальное имя из алфавита.

В операции слияния цветных сетей по местам, необходимо убрать расщепление мест по токенам с определёнными именами. Фактически, это означает переопределение операции слияния по одной s-точке доступа в простых сетях в операцию слияния серии точек доступа цветных сетей, пронумерованных значениями параметров с именами. Можно показать, что изменённая таким образом операция не меняет своих свойст.

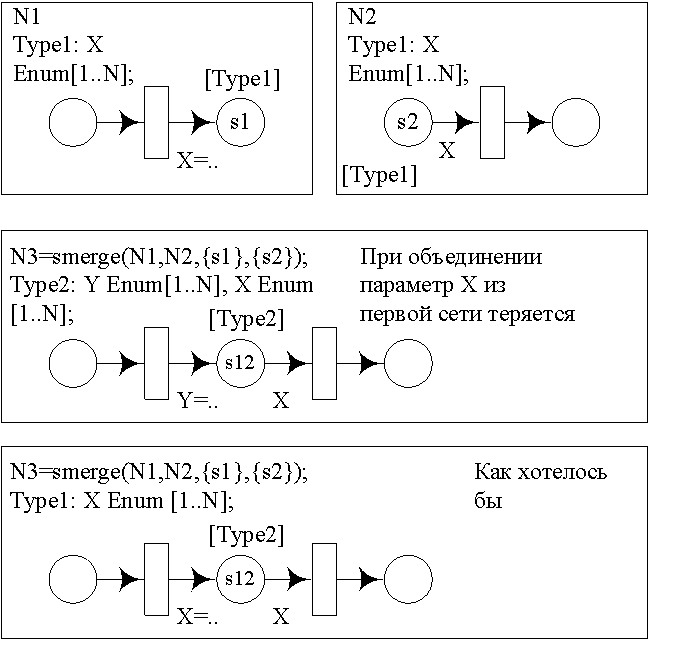
Рис. 7: Пример слияния цветных сетей Петри по S-точке доступа

T-точка доступа. При синхронизации по t-точке доступа используется информация о пометке переходов, участвующих в синхронизации. При преобразовании цветных сетей в простые, переходы расщепляются на количество, равное мощности множества значений принимаемых всеми токенами, поступающими в переход. В связи с этим возникает возможность параметризации пометки перехода выражениями, содержащими переменные поступающие в переход.

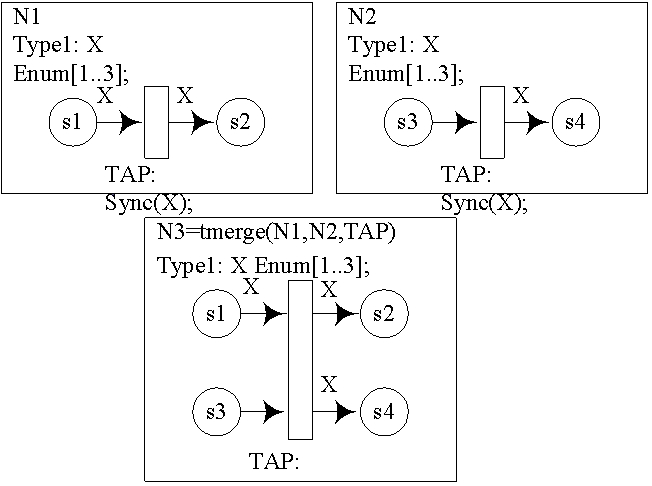
Рис. 8: Пример слияния цветных сетей по T-точке доступа

На приведённом ниже примере видно, как параметризованный переход, преобразуется в простые сети.

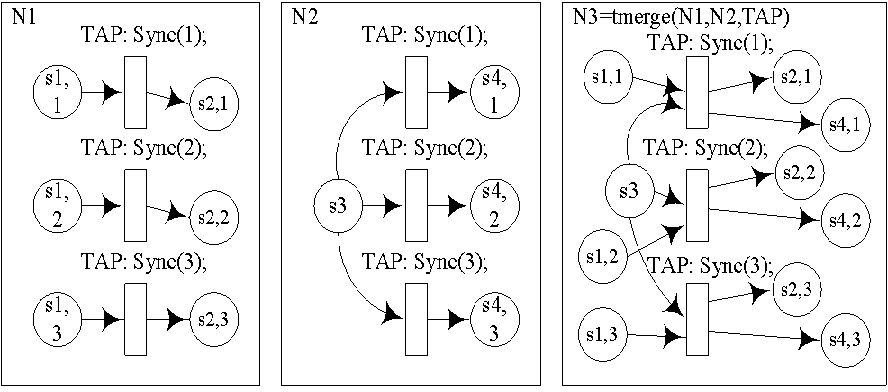
Рис. 9: T-Слияние простых сетей из рисунка 8.

Рис. 10: Представление композициональных сетей Петри на уровне взаимодействия сетей.

Дата добавления: 2014-01-05