Работа сети Петри

Выполнением (работой) сети Петри управляют количество и распределение фишек в сети. Фишки находятся в кружках и управляют выполнением переходов сети. Сеть Петри выполняется посредством запусков переходов. Переход запускается удалением фишек из его входных позиций и образованием новых фишек, помещаемых в его выходные позиции.
Переход может запускаться только в том случае, когда он разрешен. Переход называется разрешенным, если каждая из его входных позиций имеет число фишек по крайней мере равное числу дуг из позиции в переход. Фишки во входной позиции, которые разрешают переход, называются его разрешающими фишками.
Например, если позиции P₁ и P₂ служат входами для перехода T₄, тогда T₄ разрешен, если P₁ и P₂ имеют хотя бы по одной фишке. Для перехода T₇ с входным комплектом {P₆,P₆,P₆} позиция P₆ должна обладать по крайней мере тремя фишками, для того чтобы T₇ был разрешен.
Переход запускается удалением всех разрешающих фишек из его входных позиций и последующим помещением в каждую из его выходных позиций по одной фишке для каждой дуги. Переход T₃ с I(T₃)={P₂} и О(T₃)={P₇,P₁₃} разрешен всякий раз, когда в P₂ будет хотя бы одна фишка. Переход T₃ запускается удалением одной фишки из позиции P₂ и помещением одной фишки в позицию P₇ и в P₁₃ (его выходы). Дополнительные фишки в позиции P₂ не влияют на запуск T₃ (хотя они могут разрешать дополнительные запуски T₃).
Запуск перехода в целом заменяет маркировку m сети Петри на новую маркировку m'. Если какая-либо входная позиция перехода не обладает достаточным количеством фишек, то переход не разрешен и не может быть запущен.
В качестве примера рассмотрим маркированную сеть Петри, изображенную на рис.

При такой маркировке разрешены только три перехода: T₁,T₃,T₄. Переход T₂ не разрешен, так как ни позиция Р₂, ни позиция Р₃, являющиеся входами перехода T₂, не содержат ни одной фишки. Так как переходы T₁,T₃,T₄ разрешены, любой из них может быть запущен. Если запущен переход T₄, то происходит удаление одной фишки из P₅, одна фишка помещается в P₃, а количество фишек в T₄ увеличивается с двух до трех. новая маркировка, полученная в результате запуска перехода T₄, показана на рис.2:

В маркированной сети Петри, изображенной на рис.2, разрешены только переходы T₁ и T₃. При запуске перехода T₁ осуществляется удаление фишки из P₁ и помещение фишек в P₂, P₃ и P₄ (в P₄ - две фишки, так как эта позиция является кратным выходом перехода T₁). Эта операция образует маркировку, приведенную на рис.3:

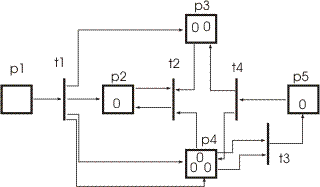
В такой маркированной сети Петри переходы T₂ и T₃ разрешены. Запуск перехода T₃ образует новую маркировку (рис.4), где две фишки удалены из P₄, а одна добавлена в P₅.

Запуски могут осуществляться до тех пор, пока существует хотя бы один разрешенный переход. Когда не останется ни одного разрешенного перехода, выполнение прекращается.

Дата добавления: 2014-01-05