Динамика - наука о наиболее общих законах взаимодействия материальных тел. Началом современной динамики является закон инерции Галилея, он же 1 закон Ньютона

Основные положения динамики.

В кинематике никакой принципиальной разницы между различными системами отсчета нет, и все они в этом отношении равноправны. Иначе обстоит дело в динамике, где изучаются законы движения. Здесь обнаруживается существенное различие между разными системами отсчета и преимущества одного класса систем отсчета по сравнению с другим. Утверждение, что инерциальные системы отсчета (ИСО) существуют, составляет содержание первого закона классической механики - закона инерции Галилея - Ньютона: существуют системы отсчета, называемые инерциальными, в которых при отсутствии воздействия других тел частица сохраняет стационарное состояние движения: движется равномерно и прямолинейно (в частном случае - покоится).

В ИСО отсчета законы механики выглядят наиболее просто.Часто за такую систему принимают гелиоцентрическую, т.е. связанную с Солнцем или геоцентрическую, связанную с Землей. Если выбрана одна ИСО., то существует множество инерциальных систем, т.к. любая система, двигающаяся по отношению к выбранной с постоянной скоростью, будет являться инерциальной.

Воздействие одного тела на другое называют силой. Действие силы вызывает ускорение тела. Сила – является количественной мерой действия одного тела на другое.

Опыт показывает, что всякое тело "оказывает сопротивление" при любых попытках изменить его скорость, как по модулю, так и по направлению. Это свойство, выражающее степень сопротивления тела к изменению его скорости, называют инертностью. У различных тел оно проявляется в разной степени. Масса m – является количественной характеристикой инертных свойств тела. Она показывает, как тело реагирует на внешнее воздействие и не зависит от того, где находится наш физический объект.

2 закон Ньютона связывает силу и параметры движения, одним из которых является ускорение.

Ускорение материальной точки в инерциальной системе отсчета прямо пропорционально действующей на точку силе, обратно пропорционально массе точки и по направлению совпадает с силой 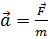. Речь идет о результирующей силе, которая является векторной суммой всех приложенных сил.

Первый закон вытекает из второго закона. Но важность его в том, что он постулирует наличие ИСО.

Принцип относительности Галилея-Ньютон а. Рассмотрим 2 инерциальные системы отсчета, вторая система отсчета двигается относительно первой с постоянной скоростью V вдоль оси х (рис.1.4.). Эти системы связаны соотношениями ;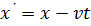
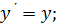
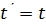, которые называются преобразованиями Галилея.

Определим законы движения тела массой 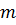в одной и другой системах отсчета 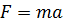и 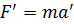. Используя второй закон Ньютона и формулы преобразования Галилея, приходим к выводу, что силы одинаковы в обеих системах отсчета . Это свойство называется инвариантностью закона Ньютона по отношению к преобразованиям Галилея. Т.е. если законы Ньютона выполняются в какой-либо системе отсчета, то они выполняются во всех системах, двигающихся относительно этой с постоянной скоростью. Таким образом, закон Ньютона совершенно одинаков в обеих (инерциальных) системах отсчета. Можно дать следующее определение инерциальных систем отсчета:

Системы, в которых справедливы законы Ньютона, называются инерциальными.

Мы можем наблюдать только относительную скорость. Находясь в поезде, движущемся с постоянной скоростью, нельзя сказать, двигается ли поезд или покоится (если не смотреть в окно). В этом состоит принцип относительности движения. Во многих практических задачах за инерциальную систему отсчета принимают систему отсчета, связанную с Землей. Тогда любая система отсчета, двигающаяся с постоянной скоростью по отношению к Земле, будет являться инерциальной. Все эти положения формулируются в виде принципа, который называется принципом Галилея-Ньютона.

Принцип Галилея-Ньютона включает в себя три основных положения:

1. Существуют такие системы отсчета, в которых, если результирующая сила, действующая на тело равна 0, то тело двигается равномерно и прямолинейно. Такие системы называются инерциальными.

2. Все ИСО по своим механическим свойствам эквивалентны друг другу. Это значит, что никакими механическими опытами, проводимыми "внутри" данной инерциальной системы, нельзя установить, покоится эта система отсчета или движется. Во всех инерциальных системах отсчета свойства пространства и времени одинаковы, одинаковы также и все законы механики.

3. Переход с одной ИСО к другой осуществляется с помощью классических преобразований - преобразований Галилея.

Принцип Галилея - один из важнейших принципов классической механики. Он является обобщением опыта и подтверждается всем многообразием приложений классической механики к движению тел, скорости которых значительно меньше скорости света.

Импульс тела. Первоначальная формулировка второго закона звучит несколько иначе. Если на тело массой m в течение некоторого малого промежутка времени Δt действовала сила 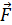, то под действием этой силы тело двигалось с ускорением а и скорость тела изменилась на ,

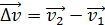Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела (или количеством движения). Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с).

Второй закон Ньютона может быть сформулирован следующим образом: изменение импульса тела (количества движения) равно импульсу силы.

Обозначив импульс тела буквой р, второй закон Ньютона можно записать в виде: 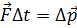, Именно в таком общем виде сформулировал второй закон сам Ньютон. Сила в этом выражении представляет собой равнодействующую всех сил, приложенных к телу. Эта формулировка имеет более общий характер и применима и в случае движения со скоростями, близкими к скорости света. В дифференциальной форме закон можно записать в виде:. Одним из видов взаимодействия тел является гравитационное взаимодействие. описываемое законом всемирного тяготения Ньютона, который гласит, что сила гравитационного притяжения между двумя материальными точками массы m₁ и m₂, разделённых расстоянием R есть ; где G — гравитационная постоянная, равная 6.67300∙10^-11м³кг^-1с^-2. Гравитационное взаимодействие приводит всегда к притяжению любых тел.

Фигурирующая в законе физическая величина – масса, характеризующая степень гравитационного взаимодействия между физическими объектами, называется гравитационной. Таким образом, в классической физике существует два понятия массы – гравитационная и инертная, которые не обязаны быть пропорциональны друг другу. Тем не менее, многочисленные эксперименты показывали равенство этих масс, теоретическое равенство этих масс было обосновано Эйнштейном в теории относительности и известно как принцип эквивалентности масс. Масса подчиняется принципу аддитивности – масса системы физических объектов равна сумме масс всех объектов, входящих в систему.

Силу тяжести mg с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни. Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору или подвес. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Понятие невесомости не включает в себя отсутствие силы тяжести, оно означает отсутствие реакции опоры или подвеса вследствие их отсутствия.

Еще раз подчеркнем, что формально второй закон Ньютона включает как частный случай первый закон Ньютона, однако первый закон Ньютона имеет более глубокое физическое содержание – он постулирует существование инерциальных систем отсчета.

3 закон Ньютона. Первый и второй законы механики относятся соответственно к движению материальной точки или одного тела. При этом учитывается лишь действие других тел на данное тело. Однако всякое действие есть взаимодействие. Поскольку в механике действие характеризуется силой, то если одно тело действует на другое с определенной силой, то второе действует на первое с той же силой, что и фиксирует третий закон механики. Во всех случаях, когда какое-либо тело действует на другое, имеет место не одностороннее действие, а взаимодействие тел. Силы такого взаимодействия между телами имеют одинаковую природу, появляются и исчезают одновременно. При взаимодействии двух тел оба тела получают ускорения, направленные по одной прямой в противоположные стороны. Опытным путем установлено: a₁/a₂=m₂/m₁, следовательно, m₁a₁=m₂a₂, или в векторном виде: 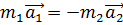или .

Последнее равенство выражает третий закон Ньютона: Тела взаимодействуют друг с другом силами, равными по модулю и противоположными по направлению.

При применении третьего закона Ньютона важно помнить:

· Силы всегда возникают парами, - если одно тело действует на другое, то и оно в свою очередь действует на первое тело;

· Силы имеют одну природу;

· Каждая из сил взаимодействия приложена к тому телу, на которое она действует, т. е. эти силы приложены к разным телам. Следовательно, силы взаимодействия между телами не могут уравновесить (скомпенсировать) друг друга.

В формулировке Ньютона третий закон механики справедлив лишь для случая непосредственного взаимодействия сил или при мгновенной передаче действия одного тела на другое. Например, проводник с током действует на движущийся заряд, заряд не действует на проводник с током.

Динамика вращательного движения материальной точки. Движение по криволинейной траектории всегда связано с наличием ускорения, следовательно, всегда существует сила, вызывающая это движение. При равномерном движении по окружности ускорение, а значит и сила, направлены по радиусу к центру окружности. Примером такого движения является вращение Луны вокруг Земли под действием силы гравитации или движение по орбите искусственного спутника Земли. Согласно 2 закону Ньютона: 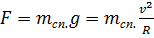, принимая за минимальный радиус орбиты радиус Земли можно вычислить 1-ю космическую скорость, необходимую для вывода спутника на орбиту:
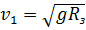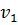, =7,9 км/с.

Сила, вызывающая равномерное движение по окружности, называется центростремительной. Необходимо обратить внимание, что данный термин указывает только на направление силы (ускорения), физическая природы центростремительной силы может быть самой разной – сила гравитации, сила Кулона, сила натяжения и т.д.

В общем случае направление силы носит произвольный характер. вектор силы можно разложить на нормальную и тангенциальную составляющие. Под действием тангенциальной составляющей точка двигается с угловым ускорением. Для массы m, вращающейся вокруг точки О по окружности радиуса R, под действием результирующей силы в инерциальной системе отсчета справедлив 2 ^ой закон Ньютона. Запишем его применительно к произвольному моменту времени: 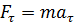, поскольку a_τ = ε·R, то умножив левую и правую части уравнения скалярно на R, получим: F_τ·R=m·ε·R²

Величина, равная векторному произведению радиус-вектора и силы: называется моментом силы относительно закрепленной точки. - радиус вектор точки приложения силы. Момент сил – величина векторная. Роль массы при вращательном движении, т.е. характеристики инертности материальной точки, играет величина J=m·R², которая называется моментом инерции.

2 закон Ньютона для вращательного движения имеет вид: произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку.

Динамика твердого тела. Твердое тело можно представить как совокупность масс, которые можно считать материальными точками. При поступательном движении все элементарные массы твердого тела движутся с одинаковыми скоростями и ускорениями и уравнение движения (2 закон Ньютона) для твердого тела совпадает с аналогичным уравнением для материальной точки. Таким образом, при поступательном движении твердое тело ведет себя так, как будто вся его масса сосредоточена в одной точке. Этой точкой является центр масс, координаты которого определяются по формулам: ; где: где m_i и x _i, y_i - массы и соответствующие координаты материальных точек (тел), входящих в систему.

При поступательном движении тела все его точки движутся с таким же ускорением, которое получает центр масс этого тела под действием равнодействующей внешних сил. Следовательно, для того чтобы описать поступательное движение тела, необходимо описать движение центра масс этого тела под действием равнодействующей внешних сил.

Для состояния покоя материального тела необходимо равенство нулю не только результирующей силы, но и момента сил, действующего на тело. 1-ый закон Ньютона для вращательного движения тела, закрепленного на оси приобретает формулировку: Тело находится в состоянии покоя или равномерно вращается, если результирующий момент сил, действующий на тело равен 0.

Под действием момента сил тело будет вращаться с угловым ускорением ε

2-ой закон Ньютона для вращательного движения тела, закрепленного на оси имеет вид M=εJ - произведение момента инерции тела на его угловое ускорение равно суммарному моменту внешних сил, действующих на тело. Моменты сил и инерции берутся относительно оси, вокруг которой происходит вращение

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется физическая величина J, равная сумме произведений масс всех i материальных точек системы на квадраты их расстояний до оси: J = m_i·r_i²

Осевой момент инерции тела является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении. Момент инерции относительно оси, проходящей через центр масс, определяется формой тела. Произвольное движение твердого тела можно рассматривать как поступательное движении центра масс и вращение тела вокруг оси, проходящей через центр масс.

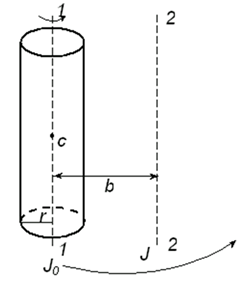
Теорема Штейнера. Момент инерции данного тела относительно, какой либо данной оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси.

	Рис. 1.5.. Момент инерции относительно произвольной оси.

Согласно теореме Гюйгенса - Штейнера - момент инерции тела J относительно произвольной оси 2-2 (рис.1.5) равен сумме момента инерции этого тела J₀, относительно оси, проходящий через центр масс этого тел1-1, и параллельной рассматриваемой оси, и произведения массы тела на квадрат расстояния между осями. J .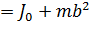

Основное уравнение динамики вращательного движения тела можно представить в виде 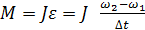или .

Момент импульса - физическая величина, равная произведению момента инерции тела I на угловую скорость его вращения ω, носит название момента импульса и обозначается буквой L: L= J∙ω. Основной закон вращательного движения приобретаеет вид: .

Статикой называется раздел механики, изучающий условия равновесия тел. Эти условия вытекают из законов Ньютона. Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс. Чтобы тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения.

Классическая механика и теория относительности.

Сложение скоростей. В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта S была равна 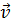, а скорость системы отсчёта S' относительно системы отсчёта S равна 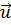, то скорость тела в при переходе в систему отсчёта S' будет равна .

Для скоростей, близких к скорости света преобразования Галилея становятся несправедливы. При переходе из системы S в систему S' необходимо использовать преобразования Лоренца: 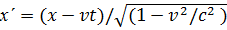; ; 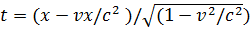где с скорость света. Формула сложения скоростей для скоростей приобретает вид: в предположении, что скорость направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Скорость зависит от выбора системы отсчета, т.е. она величина неинвариантная (инвариантными называются величины, которые не зависят от системы отсчета). Для решения задач это часто удобно, так как можно выбрать систему отсчета, в которой скорость = 0, тем самым облегчая математическое решение задачи. Но, если положить v=c, то 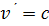, скорость света не зависит от системы отсчета, т.е. является величиной инвариантной. Это положение является одним из постулатов теории относительности. (второй постулат утверждает равенство всех законов физики в инерциальных системах отсчета). Согласно теории относительности предельная скорость движения физического объекта равна скорости света, т.е. ≈ 300000 км/с.

Согласно представлениям классической физики масса зависит только от свойств самого тела, т.е. является величиной постоянной. Тогда из выражения 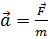следует, что если на тело действует постоянная сила, то тело двигается с ускорением, т.е. его скорость может неограниченно возрастать. Однако, по представлениям современной физики, в частности теории относительности, скорость любого движущегося объекта не может быть больше скорости света и с увеличением скорости масса тела возрастает: m 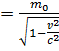, где 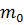- масса покоя. Формулировка второго закона, включающая импульс 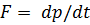является более правильной.

Дата добавления: 2014-01-05