Механические методы измерения силы, массы

Диапазон масс материальных тел огромен - от 9.1*10^-31 кг (масса электрона) до 10³⁰ кг (масса солнца). Для определения массы различных материальных объектов применяют различные методы.

Измерение массы. Масса – физическая величина, входит в два несвязанных основных закона: 2-ой закон Ньютона и закон гравитации.

Масса – мера инертности, свойство тела реагировать на попытку воздействия (силы), определяется вторым законом Ньютона F=ma. Инерционную массу можно определить с помощью закона сохранения импульса. Так в свое время Резерфорд определил массу ядра атома мишени.

Масса гравитационная – ^.мера гравитационного взаимодействия. Тело гравитационной массы m притягивается тело к Земле с силой, определяемой законом гравитации ; вес тела Р=mg. Т.к. гравитационная масса и инертная массы совпадают, то инерционную массу можно определять как гравитационную массу, т.е. путем взвешивания.

Как следствие существует 2 способа определения массы.

1. Измерение веса. Так как в данной точке Земли ускорение свободного падения g=const., то взвешивание можно производить путем сравнивания с эталоном. Метод используется для макроскопических объектов.

2. Определение инерционной массы. Используется чаще всего для определения массы заряженных частиц.

Гравитационные методы измерения масс. Взвешиванием называют метод измерения массы тела с использованием эффекта гравитационных сил, действующих на тело. Его взвешивают на весах, которые разделяют на группы: рычажные, пружинные, электронно-механические и т. д.., На пружинных и прочих весах определяют силу тяжести взвешиваемого груза, по которой судят о его массе.

1. метод сравнение масс. Наиболее распространены рычажные весы, их действие основано на законе равновесия рычага. Один из основных элементов рычажных весов — рычаг. Твердое тело, способное под действием внешних сил, приложенных к нему в одной плоскости, поворачиваться на произвольный угол, называют рычагом. Рычагом первого рода называют рычаг, у которого линии действия приложенных к нему сил проходят по обеим сторонам от точки опоры

Примером весов, в которых используют рычаги первого рода, могут быть коромысловые весы (рис.1.6а). Рычагом второго рода называют рычаг, в котором линии действия всех приложенных к нему сил проходят с одной стороны от точки опоры (рис.1.6.б).

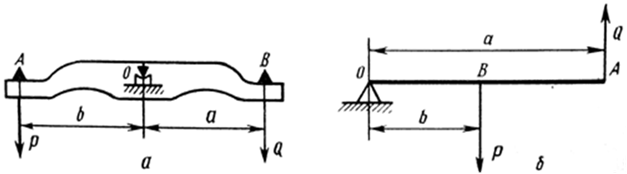Рис.1.6. Рычаг 1рода (а) и 2-го рода (б)

Частным случаем состояния, в котором может находиться рычаг, будет состояние покоя, или равновесия. Рычаг находится в равновесии тогда, когда сумма моментов всех приложенных сил относительно точки опоры равна нулю. Математически это записывается следующим образом:

На рычаги, используемые в весах, обычно действуют две внешние силы, поэтому уравнение моментов имеет простой вид. Например, для рычага первого рода уравнение записывают в виде

В уравнении момент M₁ — это момент силы Q на плече а относительно опоры 0, а M2 — момент силы Р на плече b. Этот момент взят со знаком минус, так как старается повернуть рычаг в сторону, противоположную движению часовой стрелки. Плечо силы (плечо рычага) для рычагов первого и второго рода определяют как расстояние от точки приложения силы (острия призмы) до точки опоры. Коромысло весов находится в равновесии в двух случаях. Первый случай b < а; тогда для равновесия рычага необходимо, чтобы сила Р была больше силы Q на отношение а/b, т. е. 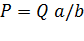, если а < b, то наоборот. Из полученных выражений, вытекает правило: для равновесия рычага необходимо, чтобы отношение внешних сил, приложенных к рычагу, было обратно пропорционально отношению плеч, или, что то же самое, во сколько раз одно плечо длиннее другого, во столько раз и сила, действующая на этом плече, должна быть меньше силы, действующей на коротком плече.

Второй случай плечо b = а; для равновесия рычага необходимо, чтобы силы Р и Q были равны. Т.о. масса гирь в нулевом положении равноплечных весов является количественной мерой измеряемой массы, для неравноплечих весов надо учитывать передаточное отношение.

Многие рычажные весы (например, торговые, автомобильные, порционные и др.) представляют собой комбинацию рычагов 1-го и 2-го родов. Опорами рычагов служат обычно призмы и подушки из специальных сталей или твёрдого камня (агат, корунд).

Метод противодействующей силы. Если тело находится в покое, то его вес согласно третьему закону Ньютона уравновешивается силой реакции Р=mg=R. В случае твердых тел в качестве этой силы выступает сила упругости. Для пружины сила упругости в соответствии с законом Гука пропорциональна смещению материальной точки из положения равновесия и направлена к положению равновесия: -к∆l, где к коэффициент упругости (жесткости), ∆l – величина растяжения (сжатия) пружины при упругой деформации.

В преобразователях силы чаще всего используются динамометры с промежуточным преобразованием силы в перемещение - пружины (рис.1.7). В пружинных динамометрах измеряемая сила уравновешивается силой упругости пружины, которая пропорциональна удлинению пружины. Регистрируя величину удлинения пружины, определяют измеряемую силу. Если такой силой является вес тела, то можно определить его массу.

Малые деформации усиливаются и фиксируются с помощью редукторных или рычажных преобразователей, гидравлических устройств или преобразуются в электрические величины.

Таким образом, метод противодействующей силы одинаково применим, как для измерения массы, так и измерения силы, при этом происходит преобразование измеряемой механической величины в перемещение, которое и является мерой этой физической величины.

1.4. Применение законов сохранения в физических измерениях

Если действующая на тело сила F вызывает его перемещение s, то действие этой силы характеризуется величиной, называемой работой.

Механической работой А называют скалярную величину, равную скалярному произведению силы на перемещение т.е. произведению модуля силы и модуля перемещения на косинус угла между направлениями силы и перемещения А=Fsсоsa. Если угол между приложенной силой и перемещением равен 90⁰, то совершаемая это силой работа равна 0. Например, центростремительная сила не совершает работу.

В СИ за единицу работы принята работа силы 1 Н при перемещении точки ее приложения на 1 м. Эта единица имеет наименование джоуль (Дж): 1 Дж = 1Н·1м.

Энергия и работа связанные между собой понятия, единицей для их измерения служит Джоуль [Дж].

Если тело некоторой массы m двигалось под действием приложенных сил, и его скорость изменилась, то силы совершили определенную работу A. Между изменением скорости тела и работой, совершенной приложенными к телу силами, существует связь. При движении тела вдоль прямой линии под действием постоянной тело совершает прямолинейное равноускоренное движение. Работа силы A = Fs. При равноускоренном движении перемещение s выражается формулой 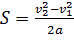, A

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела: ,

Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью v равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость: .

Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.

В природе существуют такие взаимодействия, что порождаемые ими силы обладают следующим свойством: работа этих сил при перемещении тела зависит только от начального и конечного положения тела и не зависит от выбранного пути. Как следствие, работа таких сил по замкнутому пути равна нулю. Такие силы называют консервативными или потенциальными. Примером консервативных сил может служить гравитационная сила. При движении тела в однородном гравитационном поле совершаемая работа равна: A=mg(h₁-h₂)=-(mgh₂-mgh₁). Рис. 1.8 иллюстрирует независимость работы гравитационной силы от пути. Если тело, падающее с высоты h ₁ до высоты h ₂ , затем опять поднимается на высоту h ₁ , совершаемая при этом работа равна нулю.

Другим примером консервативной силы может служить электростатическая сила притяжения или отталкивания электрических зарядов или упругая сила сжатой пружины. Пример неконсервативных сил: сила трения.

Работа, совершаемая при движении в гравитационном поле, равна изменению некоторой физической величины mgh, взятому с противоположным знаком. Эту физическую величину называют потенциальной энергией тела в поле силы тяжести E_p = mgh. Потенциальная энергия - некоторая функция, описывающая взаимное расположение тел в системе, изменение которой взятое с обратным знаком, равно работе потенциальных сил, действующих между телами системы.

Свойства потенциальной энергии:

· это энергия системы тел, между которыми действуют потенциальные силы взаимодействия;

· потенциальная энергия определяется с точностью до постоянного слагаемого. При этом за нулевой уровень потенциальной энергии можно принять любое состояние системы; Потенциальная энергия E_p зависит от выбора нулевого уровня, то есть от выбора начала координат оси OY. Физический смысл имеет не сама потенциальная энергия, а ее изменение ΔE_p=E_p2–E_p1 при перемещении тела из одного положения в другое. Это изменение не зависит от выбора нулевого уровня.

· формула для расчета потенциальной энергии может быть разной и зависит от характера взаимодействия тел;

· общим для всех видов потенциальной энергии является ее связь с работой потенциальных сил A_{пот. сил} = - (E_п2 - E_п1), т.е. работа потенциальных сил равна изменению потенциальной энергии, взятой со знаком минус.

Закон сохранения механической энергии. Работа, совершаемая консервативными силами, действующими на тело, равна, с одной стороны, изменению кинетической энергии тела, а с другой - взятому со знаком минус изменению потенциальной энергии. Поэтому Е_к2-Е_к1=-(Е_р2-Е_р1) или Е_к1+Е_р1=Е_к2+Е_р1. Таким образом, для отдельно взятого тела сумма кинетической и потенциальной энергии этого тела сохраняется в процессе движения.

Замкнутой системой называют группу тел, не взаимодействующих ни с какими другими телами, которые не входят в состав этой группы. Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона. Сумму E=E_k+E_p называют полной механической энергией. Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии. Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.

Закон сохранения импульса. При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. По третьему закону Ньютона 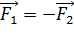. Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны: . 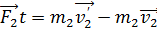По второму закону: ; где ; ,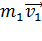

Дата добавления: 2014-01-05