Аналитическое решение линейных и нелинейных систем уравнений

Лекция

Однопартийные режимы

4. Государство как политический институт

Признаки государства:

1. Территория

2. Население

3. Публичная власть

4. Суверенитет

5. Монопольное право на принуждение

6. Монопольные права на налоги

7. Законотворчество

к занятию №3

Тема: Типы данных в MathCAD

План:

1. Решение систем линейных уравнений с методом обратной матрицы.

2. Решение уравнений и систем уравнений с помощью блока Given-Find.

3. Аналитическое решение линейных и нелинейных систем уравнений.

Пример матричных вычислений: решение системы линейных алгебраических уравнений методом обратной матрицы

Допустим, что необходимо решить следующую систему уравнений:

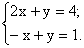
Воспользуемся матричным методом, когда решение находится по формуле X = A^-1B, где A - матрица коэффициентов при переменных системы; B - вектор свободных членов. Поскольку в MathCAD нет понятия вектора, используется матрица из одного столбца. На листе MathCAD (рис. 1) необходимо определить эти матрицы, записать формулу для X и подсчитать X, применив оператор числового вычисления «=».

Рисунок 1 - Вид листа MathCAD при решении данной задачи

Решение уравнений и систем уравнений с помощью блока Given-Find

Решение систем уравнений MathCAD осуществляет численными методами. При этом должно быть задано некоторое начальное приближение для тех переменных, значение которых необходимо найти. Основываясь на этих начальных данных, MathCAD будет последовательно уточнять решение до тех пор, пока не подберет наиболее точные значения. Проблемы возникают, когда нелинейная система имеет несколько решений. За один раз MathCAD находит только одно решение, которое обычно более близко к заданному начальному приближению. Поэтому в таких случаях необходимо решать систему несколько раз с различными начальными приближениями.

Решающий блок состоит из нескольких компонент, следующих на листе в строго определенном порядке:

1. Начальное приближение (присваивание начальных значений переменным).

2. Директива Given, которую необходимо набрать с клавиатуры.

3. Уравнения (уравнение), которые необходимо решить. Уравнения вводятся в обычной математической форме, но вместо простого знака равенства «=» используется оператор логического равенства (вводится путем нажатия Ctrl-=).

4. Обращение к функции Find. Аргументами функции являются имена переменных, относительно которых решается система. Функция возвращает вектор значений, где первый элемент соответствует первой переменной в списке аргументов, второй элемент - второй переменной и так далее.

Пример. Решим систему нелинейных уравнений:

Данная система имеет два решения. Найдем одно из них (рис. 2) с начальным приближением x = 0; y = 0.

Рисунок 2 - Решение системы в MathCAD

Последняя запись - вектор (-1; -2) есть значение, которое вернула функция Find, то есть одно из решений системы. Найти второе решение можно, если взять другое начальное приближение x = 2; y = 2. Тогда функция Find вернет вектор (2; 4).

Начиная с MathCAD 2000 существует возможность одновременно найти несколько решений. Для этого система уравнений и начальные приближения должны быть переписаны в векторной форме (рис. 3). Каждая переменная будет вектором, содержащим столько компонент, сколько решений находится. В системе изменения коснутся преимущественно членов с перемножением переменных. Допустим, что в уравнении присутствует выражение x*x. Если x = (x₁; x₂) - вектор, то . Нам же необходим результат поэлементного перемножения 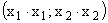. Для этого существует специальная операция, записываемая как .

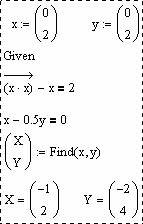
Рисунок 3 - Пример одновременного поиска нескольких решений

Изменения коснулись и части получения результата. В данном случае функция Find вернет вектор из двух элементов, которые мы обозначили как X и Y. Каждый из этих элементов есть вектор значений x или y для решений. Соответственно первое решение - (-1; -2); второе решение - (2; 4).

Пример. Решим уравнение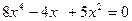

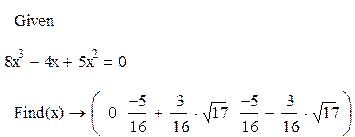
Пример. Решим систему линейных уравнений

і	аі1	аі2	аі3	bі
	2.91 0.31 0.61	-1.15 4.55 -0.33	-1.33 2.45 3.21	5.401 4.031 11.23

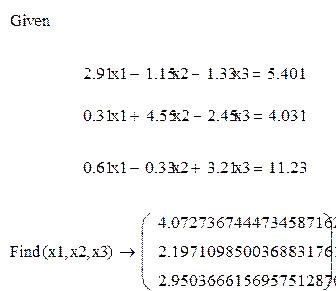
Пример. Решим систему не линейных уравнений

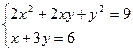
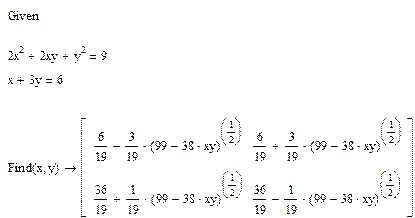
Данное решение используется для получения решений в общем виде. Обычно при этом система уравнений записывается только с использованием буквенных обозначений переменных, без конкретных чисел. Для получения аналитического решения (рис. 4, 5) используется оператор аналитического вычисления «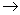» вместо оператора числового вычисления «=».

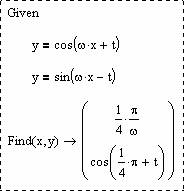
Рисунок 4 - Пример аналитического решения нелинейной системы

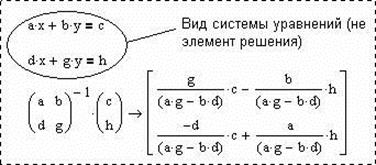
Рисунок 5 - Пример аналитического решения линейной системы

Следует обратить внимание, что здесь при решении системы нелинейных уравнений в блоке Given-Find уже нет необходимости указывать начальные приближения, поскольку решение идет не численными, а символьными методами (используется ядро математической системы Maple).

Контрольные вопросы:

1. Какие переменные называются ранжированными?

2. Как работать с ранжированными переменными?

3. Как решаются уравнения в МаthCad?

4. Как решаются системы уравнений в МаthCad?

5. Что такое аналитическое решение системы уравнений?

Дата добавления: 2014-01-05