Получим общие уравнения движения жидкости, устанавливающие связь между внешними и внутренними силами, действующими на нее

Уравнения движения жидкости в напряжениях

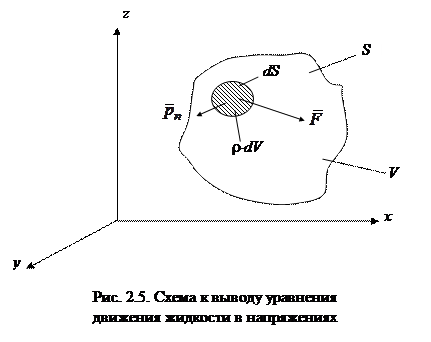
Выделим в движущейся жидкости поверхностью S произвольный жидкий объем V (рис. 2.5), а внутри него – элементарную жидкую частицу с массой pdV и поверхностью dS. К этой частице приложены массовые силы с напряжением F и поверхностные силы с напряжением р_п. Запишем уравнение движения этой частицы, обозначая ускорение ее центра тяжести :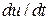

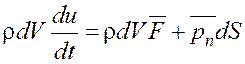. (2.24)

Просуммируем левую и правую части уравнения (2.24). Суммирование первых двух членов сводится к интегрированию по объему, а третьего члена – по площадкам, которыми элементарные частицы соприкасаются друг с другом. Согласно третьему закону Ньютона поверхностные силы по всем внутренним площадкам взаимно уничтожатся и останутся только поверхностные силы по площади S, ограничивающей объем V:

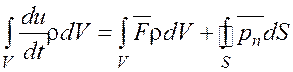z. (2.25)

Здесь и в дальнейшем кратные интегралы будут различаться только индексом, по которому производится суммирование. Преобразуем третий член уравнения (2.25), используя для этого зависимость (2.15),

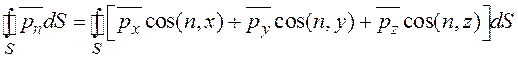. (2.26)

Применим к правой части этого равенства известное преобразование Гаусса-Остроградского, устанавливающее связь между объемным и поверхностным интегралами,

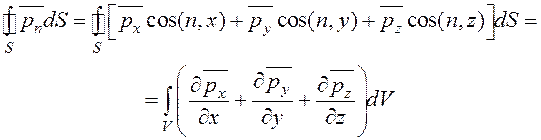. (2.27)

Подставляя правую часть (2.27) в уравнение (2.25), получим:

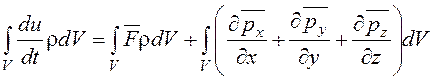. (2.28)

Все члены в уравнении (2.28) интегрируются по объему. Уравнения (2.25) и (2.28) являются уравнениями движения жидкого объема в интегральной форме. Их левая часть представляет главный вектор сил инерции, первый член правой части – главный вектор массовых сил, а второй – главный вектор поверхностных сил.

Получим дифференциальную форму уравнения движения, более удобную для изучения движения жидкости. Объединим все члены уравнения (2.28) под знаком интеграла, перенося силу инерции в правую часть,

.

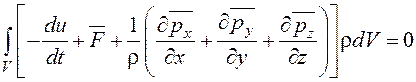Ввиду произвольности объема этот интеграл обращается в нуль только тогда, когда нулю тождественно равна подынтегральная функция:

.

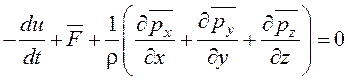В итоге получим дифференциальное уравнение движения жидкости в напряжениях:

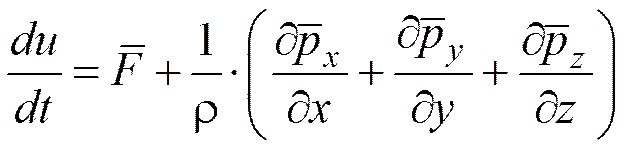, (2.29)

которое связывает ускорения с напряжениями массовых и поверхностных сил в данной точке потока и справедливо как для вязкой, так и невязкой жидкости.

Проектируя векторное уравнение (2.29) на оси координат, будем иметь:

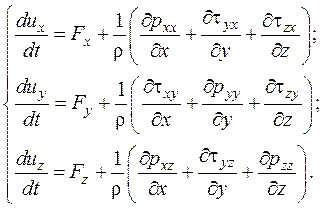(2.30)

Система уравнений (2.30) служит основой для разработки гидродинамики вязкой и невязкой жидкости.

Дата добавления: 2014-01-05