Принцип дедукции

Лекция 5

Вернемся к выражению (5.1) (H₁, H₂,... Hn) 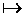B и предположим, что оно выполняется, т.е. B - выводимо из {H}. Если это так, то присоединение B к множеству {H} не влияет на полноту множества {H, B} и не приводит его к противоречию. Иное дело , которая при этих условиях невыводима. Ее присоединение к {H}, очевидно, приведет к противоречивости, т.е. можно написать:

(H₁, H₂,... Hn, ) 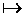Л. (5.8)

При этих условиях тождественность импликации

(H₁ Ù H₂ Ù H₃... Ù H_n)® B 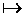И. (5.3),

естественно, нарушается, она становится невыполнимой. Возьмем отрицание импликации (5.3). Теперь должно выполняться условие

(5.9)

Доказав невыполнимость (5.8) или (5.9), мы косвенно докажем выполнимость условия (5.1). Такой метод доказательства "от противного" называется доказательством по методу опровержения.

Метод опровержения очень удобен. B самом деле, вместо того, чтобы кропотливо доказывать общезначимость какой-либо формулы F достаточно доказать невыполнимость ее отрицания ,что в ряде случаев значительно проще. (B 60-х годах ХХ века был открыт и разработан так называемый принцип резолюций, весьма подходящий для доказательств подобного рода).

Метод опровержения реализует принцип дедукции, который формулируется следующим образом:

формула B является логическим следствием множества {H} тогда и только тогда, когда множество {H, 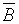} невыполнимо, т.е. (H₁, H₂,... Hn) 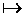B, если (H₁, H₂,... Hn, 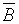) 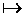Л.

Докажем условие (5.9).

Исключим импликацию:

и по правилу де Моргана получим:

,

что эквивалентно выражению

H₁ Ù H₂ Ù ... Ù Hn Ù 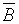. (5.10)

Дело, таким образом, сводится к доказательству невыполнимости

(H₁ Ù H₂ Ù ... Ù Hn Ù 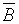) 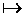Л. (5.11)

Формула (5.10) в своем виде уже является элементом КНФ, даже если все Hi - элементарные высказывания. Если же Hi - сложные выражения, то они приводимы к виду КНФ и их подстановка в (5.10) не меняет ее нормальной формы. Поэтому в дальнейшем мы вправе считать каждое из Hi дизъюнктом, состоящим из одного или многих "слагаемых".

Условие (5.11) требует, чтобы формула (5.10) была невыполнима, т.е. тождественно равна 0. Это возможно, если среди ее "сомножителей" найдется хотя бы один пустой дизъюнкт. Такой дизъюнкт не может появиться в явном виде. Но он может быть определен на множестве {H, 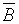} путем определенных эквивалентных преобразований.

Из всего вышесказанного следует, что, согласно принципу дедукции, вопрос о выводимости (невыводимости) некоторой формулы B сводится, в конечном счете, к анализу невыполнимости множества дизъюнктов. Но множество дизъюнктов невыполнимо тогда и только тогда, когда пустой дизъюнкт Л является логическим следствием из него. Таким образом, невыполнимость множества {H, 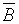} можно проверить, порождая логические следствия из него до тех пор, пока не получится пустой дизъюнкт. Метод, позволяющий получить логические следствия из множества дизъюнктов, основан на применении принципа резолюций.

Дата добавления: 2014-01-05