Взаимосвязь вероятностей ошибок первого и второго рода

Статистическая гипотеза - это любое предположение, касающееся неизвестного закона распределения случайной величины или неизвестного значения параметра этого распределения, т.е. предположение о свойствах случайной величины.

Проверка статистических гипотез

Критерии проверки статистических гипотез

Проверка статистических гипотез

План лекции

Лекция № 5

Гипотезу, подлежащую проверке, принято называть основной или нулевой (гипотеза Н_о). Гипотезу, противопоставляемую выдвинутой нулевой гипотезе, называют альтернативной или конкурирующей (гипотеза Н₁).

Для проверки статистических гипотез применяется система правил (статистических критериев), которая позволяет путем анализа выборок из генеральной совокупности принять или отвергнуть выдвинутую гипотезу

С помощью параметрических критериев проверяется гипотеза относительно значения Θ₀ параметра θ данного распределения, например гипотезы типа Н_0: Θ =_: Θ₀ или Θ ≥_: Θ₀ •

С помощью непараметрических критериев, так называемых критериев согласия, проверяют гипотезу Н_0: о виде закона распределения.

Для формулировки критерия множество значений контролируемого параметра разделяется на критическую область - область отклонения гипотезы Н_0: и дополнительную к ней область принятия гипотезы Н_0:. Если выборочное значение контролируемого параметра попадает в критическую область, гипотезу Н_0: отвергают, в противном случае ее принимают.

Из-за случайности выборочных значений контролируемого параметра такое принятие гипотезы не является доказательством ее истинности, равно как и отклонение гипотезы еще не означает, что она ложна. Здесь возможны четыре случая:

-гипотеза Н_0:верна и принимается согласно критерию;

-гипотеза Н_0: неверна и отвергается согласно критерию;

- гипотеза Н_0:верна, но отвергается согласно критерию (ошибка первого род α);

-гипотеза Н_0:неверна, но принимается согласно критерию (ошибка второго рода β).

Вероятность совершить ошибку первого рода принято обозначать через α, поэтому ее называют α -ошибкой. Причем вероятность α является уровнем значимости критерия. При выборочном приемочном контроле ошибка первого рода приводит к браковке партии продукции с допустимым уровнем несоответствий (так называемый риск производителя или поставщика), а при контроле производственного процесса - к необоснованному вмешательству в налаженный процесс производства (ложная тревога, излишнее управление).

Вероятность появления ошибки второго рода принято обозначать через β, это так называемая β-ошибка. При выборочном приемочном контроле ошибка второго рода приводит к принятию партии продукции с недопустимым уровнем несоответствий (риск потребителя или заказчика), а при контроле производства - к невмешательству в разлаженный производственный процесс (пропуск разладки, незамеченная разладка).

Вопрос о взаимосвязи вероятностей ошибок первого и второго рода и о том, влиянию каких параметров подвержены эти вероятности, рассмотрим на следующем простом примере.

Пусть при налаженном процессе значения контролируемого параметра подчиняются нормальному закону распределения с математическим ожиданием m_oи дисперсией σ_o², а в разлаженном режиме - нормальному закону с параметрами m₁ и σ₁², т.е. дисперсия в обоих режимах одинакова. Нулевой гипотезе Н₀ соответствует µ = µ_o? а единственно возможной альтернативной гипотезе Н₁ соответствует µ = µ₁

Для проверки, в каком состоянии находится процесс, берется безвозвратная выборка объемом п из потенциально бесконечной генеральной совокупности и рассчитывается выборочное среднее , которое является несмещенной оценкой параметра m_o Плотности распределения , при верности гипотез H_o и H₁ приведены на рис.

Рисунок – 1 Плотность нормального распределения выборочного среднего арифметического при верности гипотезы Н_о (кривая 1) и верности гипотезы Н₁ (кривая 2)

На этом рисунке точка µ_кр на оси абсцисс разделяет область значений контролируемой величины µ_{о <} µ_{кр <} µ₁ на критическую область Ho[µ_{кр? ∞]}- область отклонения гипотезы 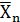и дополнительную к ней область принятия гипотезы H_o[-∞µ_кр].

Из рисунка следует, что попадание 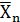в критическую область оказывается возможным и при верности гипотезы Н_о.. При этом гипотеза Н_о. ошибочно отвергается, т.е. происходит ошибка первого рода. Но также возможно попадание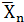в область принятия гипотезы Н_о, когда эта гипотеза неверна. В этом случае ошибочно принимается гипотеза Н_о, и совершается ошибка второго рода.

Вероятность ошибки первого рода, т.е. вероятность попадания 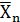в интервал [µ_кр,∞] при верности гипотезы H_o определяется соотношением)

)

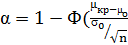а вероятность ошибки второго рода, т.е. вероятность попадания 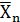в интервал [ -∞, µ_кр], при верности гипотезы H₁ определяется

соотношением

| )

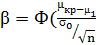Учитывая, что µ_кр - µ₁ <0 получаем

)

Из приведенных соотношений следует, что:

- увеличение объема выборки п ведет к уменьшению дисперсии выборочной средней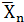и тем самым к одновременному уменьшению вероятности ошибок обоих видов;

- сумма (α+β) не равна единице. Вероятность ошибок обоих решений -принятия или отклонения гипотезы H_o -относится к различным плотностям распределения (кривые 1 и 2 на рис. 5/1);

- увеличение µ_кр ведет к уменьшению α, но к одновременному увеличению β, а уменьшение µ_крприводит к увеличению α, и уменьшению. βПодчеркнем, что одновременное уменьшение значений α и β возможно только за счет увеличения объема выборки;

- задавая значение α, т.е. уровень значимости критерия, тем самым определяем область отклонения гипотезы H_o. Наиболее распространенными значениями α являются 0,1; 0,05;0,01; 0,001;

- вероятность ошибки первого рода α относится к критерию проверки гипотез в целом, а не к отдельному результату проверки. Отсюда следует, что если проверка проводится многократно, то, примерно, в α «100% случаях гипотеза H_o может быть отклонена даже, если она в действительности верна.

При определении области отклонения гипотезы необходимо, во-первых, учитывать, что максимальная вероятность ошибки первого Рода должна быть не больше, чем заданный уровень значимости критерия, а во-вторых, вероятность ошибки второго рода должна быть как можно меньше. Вероятность ошибок обоих видов можно определить, используя оперативную характеристику критерия, которая представляет собой зависимость вероятности принятия гипотезы Р(Н_о)от неизвестного значения контролируемого параметра θ, т.е. Р(θ), и задается уравнением, таблицей или графиком (рис. 2).

Рисунок 2 Оперативная характеристика

Дата добавления: 2014-01-05