Алгоритм проверки статистических гипотез

Оперативная характеристика критерия проверки гипотезы

Вероятности ошибочного отклонения или принятия гипотезы Н₀ можно непосредственно определить по графику оперативной характеристики. При этом в области принятия гипотезы Н₀ выражение(1- Р(θ))является зависящей от θ вероятностью ошибки первого рода, а в критической области значение Р(θ) является зависящей от θ вероятностью ошибки второго рода.

В общем случае в области принятия гипотезы Н₀ оперативная характеристика должна иметь как можно большее значение, а в критической области - как можно меньшее значение.

Идеально на границе раздела критической области и области; принятия гипотезы Н₀ оперативная характеристика должна претерпевать единичный скачок. При этом статистический критерий является идеальным, а вероятности ошибок первого и второго рода равны нулю.

Таким образом, по известной оперативной характеристике Р(θ)статистического критерия для каждого значения контролируемого параметра θ можно вычислить вероятность принятия нулевой гипотезы.

Однако при применении статистических методов обеспечения качества иногда требуется по заданной вероятности принятия гипотезы Н₀ Р(θ) = ωопределить соответствующее значение контролируемого параметра θ_ω, т.е. значение соответствующей квантили оперативной характеристики порядка или уровня ω. Например, при выборочном приемочном контроле квантили позволяют определить уровни несоответствий в контролируемой партии продукции, при которых партии продукции будут приниматься с за­данной вероятностью.

Определить квантиль оперативной характеристики θ_ωможно из графика оперативной характеристики как абсциссу, соответствующую значению координаты (рис. 2), или с помощью квантильной (обратной) функции θ_ω= Р’(θ_ω). Например, с использованием таблицы значение квантили уровня 0,995 нормированного нормального распределения θ_0,995 = 2,58

В заключение отметим, что таблица значений квантилей нормированного нормального распределения приведена, например, в таблице значений квантилей нормального распределения, распределения Стьюдента, F-распределения Фишера и χ²-распределения. Значения квантилей этих распределений могут быть рассчитаны с помощью персонального компьютера и пакета статистического анализа.

Решение — принять или отвергнуть нулевую гипотезу — принимается на основе определенного критерия. При этом выбирается некоторая функция элементов выборки или статистика критерия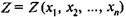, распределение которой известно.

Множество значений статистики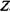, при которых принимается решение отклонить гипотезу, называется критической областью. Положение критической области определяется видом альтернативной гипотезы и заданным уровнем значимости.

Множество значений статистики, при которых нулевая гипотеза принимается, называется областью принятия решения.

Например, рассмотрим случай, когда некоторая несмещенная оценка параметра θ вычислена по выборке объема n, и эта оценка имеет плотность распределения f(θ), рис.1.

Рисунок 1 Области принятия и отклонения решений.

Пусть, например, проверяется гипотеза о том, что параметр распределения генеральной совокупности Н₀: θ = θ₀.При этом возможны различные варианты альтернативных гипотез.

Если, например Н₁: θ < θ₀, то критическая область расположена в левом «хвосте» соответствующего распределения, причем положение границы критической области определяется квантилью Z_α.

Если Н₁: θ > θ₀, то критическая область — в правом «хвосте»; ее граница определяется квантилью Z_1-α. В двух рассмотренных случаях имеем одностороннюю критическую область.

Если же альтернативная гипотеза имеет вид Н₁: θ ≠ θ₀, критическая область — двухсторонняя; ее границы определяются соответственно квантилями Z_α/2 и Z_1-α/2.

В общем случае алгоритм проверки гипотезы с помощью критерия значимости таков:

ü формулируется нулевая и альтернативная гипотезы,

ü задается уровень значимости,

ü выбирается статистика критерия для проверки сформулированной нулевой гипотезы,

ü определяется выборочное распределение этой статистики,

ü определяется положение критической области,

ü вычисляется выборочное значение статистики критерия

ü принимается статистическое решение: если выборочное значение статистики критерия оказалось в области принятия решения, нулевая гипотеза принимается; в противном случае нулевая гипотеза отклоняется, как несогласующаяся с результатами наблюдений.

Дата добавления: 2014-01-05