Критерии значимости при биномиальном распределении

Пример

Проверить гипотезу о том, что средний диаметр валиков, изготавливаемых на станке-автомате, равен т₀ = 12 мм, если по выборке из n = 16 валиков найдены среднее значение х= 11,7 мм и несмещенная дисперсия s² = 0,25 мм². Распределение диаметра валика предполагается нормальным.

Решение. Проверяется нулевая гипотеза Н₀: т = т₀ при альтернативной гипотезе H_1: т < т₀ (поскольку среднее значение оказалось меньше, чем m₀). Принимаем уровень значимости α = 0,05.

Выборочное значение статистики Стьюдента по формуле

t_B, = (11,7 -12). 4 /0,5 = -2,4.

Для левосторонней критической области положение границы

Zк_Р =Z α = t'_0,05(15) = -t_0,95 (15) = -1,753.

Рисунок 1 - Положение критической области при проверке гипотезы о диаметре валиков

Выборочное значение статистики — 2,4 попало в критическую область нулевая гипотеза о том, что средний диаметр валиков равен 12 мм, отвергается.

Часто на практике возникает задача о сравнении средних значений двух нормально распределенных совокупностей,

При проверке гипотезы Н₀: m₁ =m_2,. если соответствующие дисперсии известны, то в качестве статистики критерия принимается величина

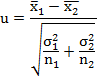
распределенная по стандартному нормальному закону.

Пример

Используя двусторонний критерий, проверить гипотезу о равенстве внутренних диаметров втулок, изготавливаемых на двух станках по одному чертежу. Из деталей, изготовленных на первом станке, отобрано n₁=12 втулок, при этом средний диаметр , на втором станке n₂=14 втулок Распределение диаметров предполагается нормальным, дисперсии известны и равны соответственно σ₁² = 0,2 мм², σ₂² = 0,25 мм²

Решение. Проверяется нулевая гипотеза Н₀: т₁ = т₂ при альтернативной гипотезе Н: т₁ ≠ т₂ (поскольку среднее значение оказалось меньше, чем m₀). Принимаем уровень значимости α = 0,05. Выборочное значение статистики Стьюдента по формуле

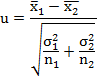
u, = (8,5 -8,3)/(0.2/12+0.25 /14)^1/2 = 1.08.

Для двусторонней критической области положение границ соответственно равно

Zк_Р1 = Z _a/2 = u_'0,025= -u _0,975 = -1,96.

Zк_Р2 = Z_{1- a/2} = u _0,975 = 1,96

Выборочное значение статистики 1,08 попало в область принятия решения (рис. 3.15), нулевая гипотеза о том, что диамет­ры втулок одинаковы, принимается.

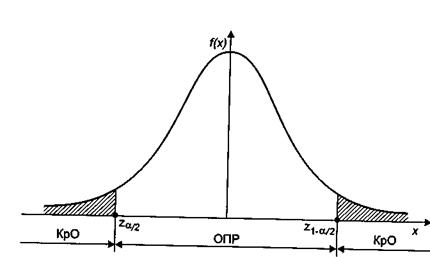
Рисунок 3-.Положение критической области при проверке гипотезы о диаметре втулок

Аналогичным образом решаются вопросы проверки гипотез о дисперсиях. В частности, если проверяется гипотеза Н₀: σ₁² = σ₂² о равенстве дисперсий двух нормально распределенных совокупностей при неизвестных математических ожиданиях, используется статистика

имеющая распределение Фишера с числами степеней свободы (n₁ - 1) и (n₂ — 1),

где n₁, и n₂ — объемы соответствующих выборок

s₁² и s₂² — несмещенные дисперсии; предполагается, что s₁² > s₂²

F – критерий Фишера, используется для установления сходства-различия дисперсий в двух независимых выборках;

Наиболее распространенной задачей проверки гипотез при биномиальном распределении, когда проводятся повторные независимые испытания, является сравнение вероятности успеха р с заданным значением р₀, т.е. нулевая гипотеза имеет вид Н₀: p = p₀ .

Предположим, что в серии из п испытаний успех имел место т раз. Тогда при определенных условиях для проверки рассматриваемой нулевой гипотезы можно использовать статистику

имеющую стандартное нормальное распределение.

Дата добавления: 2014-01-05