Характеристическая функция

Математическое ожидание и его свойства.

Числовые характеристики случайных величин.

Характеристическая функция.

Лекция №5

Раздел 2. Случайные величины.

Тема 1. Функция распределения, плотность вероятности и числовые характеристики случайной величины.

Цель лекции: дать знания о способах описания случайных величин.

Вопросы лекции:

Литература:

Л1 - Бочаров П. П., Печинкин А. В. Теория вероятностей. Математическая статистика. - 2-е изд. - М.: ФИЗМАТЛИТ, 2005. - 296 с.

Л2 - Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2005. — 479 с: ил.

Л3 - Нахман А.Д., Косенкова И.В. Ряды. Теория вероятностей и математическая статистика. Методические разработки. – Тамбов: Издательство ТГТУ, 2009.

Л4 - Плотникова С.В. Математическая статистика. Методические разработки. – Тамбов: Издательство ТГТУ, 2005. (pdf-файл)

При решении многих задач вместо функции распределения F(x) и п.в. р(х) применяется характеристическая функция . С помощью этой характеристики оказывается целесообразным, например, определять некоторые числовые характеристики сл.в. и з.р. функций сл.в.

Характеристической функцией сл.в. 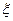называется преобразование Фурье от ее п.в. р(х):

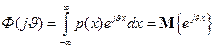, (2.6.1)

где 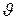- параметр, являющийся аргументом характеристической функции, 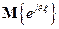- м.о. сл.в. (см § 2.8.).

Применив обратное преобразование Фурье, получим формулу, определяющую п.в. сл.в. по ее характеристической функции

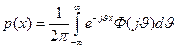. (2.6.2)

Так как размерность р(х) обратна размерности x, то величина , а следовательно, и являются безразмерными. Аргумент 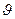имеет размерность обратную размерности x.

Воспользовавшись представлением (2.5.7) п.в. р(х) в виде суммы дельта-функций, можно распространить формулу (1) на дискретные сл.в.

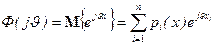. (2.6.3)

Иногда вместо характеристической функции 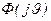оказывается удобным использовать логарифм от нее:

Y . (2.6.4)

Функцию Y 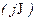можно назвать второй (логарифмической) характеристической функцией сл.в. 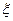[24].

Отметим наиболее важные свойства характеристической функции.

1. Характеристическая функция удовлетворяет следующим условиям:

. (2.6.5)

2. Для симметричного распределения, когда р(х)= р(-х), мнимая часть в (1) равна нулю, и, следовательно, характеристическая функция является действительной четной функцией 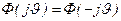. Наоборот, если 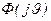принимает только действительные значения, то она четна и соответствующее ей распределение симметрично.

3. Если сл.в. 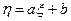является линейной функцией сл.в. 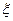, то ее характеристическая функция определяется выражением

, (2.6.6)

где a и b - постоянные.

4. Характеристическая функция суммы 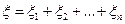независимых сл.в. равна произведению характеристических функций слагаемых, т.е., если

. (2.6.7)

Это свойство особенно полезно, так как в противном случае нахождение п.в. суммы сл.в. связано с многократным повторением свертки, что вызывает иногда затруднения.

Таким образом, учитывая однозначную связь между функцией распределения, плотностью вероятности и характеристической функцией, последняя в равной мере может быть использована для описания сл.в.

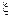Пример 2.6.1. По каналу связи с помехами передается кодовая комбинация из двух импульсов. Из-за независимого воздействия помехи на эти импульсы каждый из них может быть подавлен с вероятностью q =0,2. Необходимо определить: I) ряд распределения cл.в. - числа подавленных помехами импульсов; 2) функцию распределения 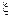; 3) плотность вероятности 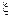; 4) характеристическую функцию сл.в. .

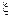Дискретная сл.в. 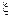может принять три значения 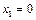(ни один из импульсов не подавлен), 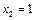(подавлен один импульс), 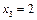(подавлены оба импульса). Вероятности 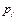этих значений соответственно равны: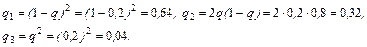

Ряд распределения в табличной форме будет иметь вид:

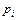
	0,64	0,32	0,04

По определению функции распределения дискретной сл.в. .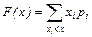

Поэтому .

Воспользовавшись формулой (2.5.7), можем записать выражение для п.в.

.

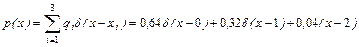Согласно формуле (З) имеем

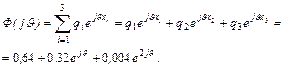
Пример 2.6.2. Сл.в. имеет равномерную п.в. в интервале от до 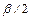. Требуется определить п.в. р(х), функцию распределения F(х) и характеристическую функцию 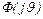cл.в. .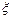

По условию нормировки, . Следовательно,

По определению

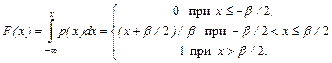
Графики п.в. р(х) и соответствующие ей функции распределения F(х) и характеристической функции приведены на рисунках 2.8,…,2.10.

Дата добавления: 2014-01-05