Общие положения. Основные законы теории пластичности

Основные законы теории пластичности

ЛЕКЦИЯ 5

Рассмотрим поведение упрочняющегося материала при нагружении и разгрузке при условии, что диаграмма деформирования при растяжении имеет вид, показанный на рис.5.1.

Если при первоначальном нагружении напряжение меньше предела текучести (точка А на рис.5.1), то материал деформируется упруго. Когда напряжение достигает предела текучести , наступает текучесть (точка В на рис.5.1). Если при первоначальном нагружении напряжения в конструкции достигнут значения 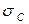, а затем произойдет разгрузка, то зависимость между напряжениями и деформациями будет определяться прямой, параллельной начальной ветви диаграммы в упругой стадии работы материала. Если нагрузку снять полностью, то в конструкции останутся пластические (необратимые) деформации . При повторном нагружении пластические деформации возникнут при напряжении 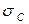, большем, чем напряжение начальной текучести. В случае простого растяжения это произойдет при достижении точки С на диаграмме , а в случае сложного напряженного состояния – при достижении некоторой точки на гиперповерхности, определяемой формулой

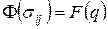
(5.1)

и называемой поверхностью текучести.

В формуле (5.1) - возрастающая функция некоторого параметра q, называемого параметром упрочнения Поверхность текучести расширяется и смещается. Если в качестве параметра q принимается накопленная пластическая деформация, определяемая формулой

,

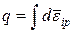(5.2)

то упрочнение называется деформационным; если в качестве этого параметра принимается работа пластических деформаций

,

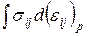(5.3)

то упрочнение называется энергетическим.

При использовании условия Губера-Мизеса формула (5.1) принимает вид:

.

(5.4)

Возводя в квадрат левую и правую части последнего выражения и учитывая формулу (4.4), получаем условие текучести в следующем виде:

.

(5.5)

Уравнение (5.5) по форме напоминает условие начала текучести (4.4). Однако смысл этого уравнения несколько иной. Оно представляет гиперповерхность текучести с учетом упрочнения материала при нагрузках, вызывающих деформацию материала за пределами первоначальной текучести. Геометрическая интерпретация гиперповерхности текучести показана на рис.5.2, где для сравнения приведена также гиперповерхность начальной текучести .

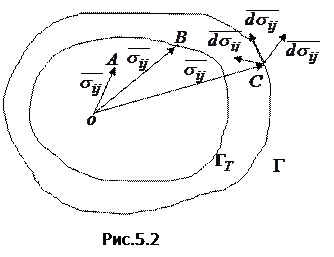
Точки А, В и С на рис.5.2 имеют тот же смысл, что и на диаграмме рис.5.1 для простого растяжения. Если в состоянии С компоненты тензора напряжений получают приращения , то возможны три варианта дальнейшего деформирования. Если вектор направлен внутрь поверхности пластичности, происходит упругая разгрузка; если он направлен наружу – развиваются пластические деформации; если же вектор лежит в плоскости, касательной к поверхности пластичности, то нагружение называется нейтральным, материал при этом деформируется упруго.

Дата добавления: 2014-01-05