Позиционную симметрию всех атомов (групп)

При этом используются два метода: позиционной симметрии (его еще называют сайт-групповым) и фактор групповой (известного также под названием метода Багавантама-Ванкатарайду.

Сайт–групповой метод (метод позиционной симметрии)

Базируется на положениях:

что нейтральная или ионная молекула, входящая в состав кристаллической элементарной ячейки, не может приобрести симметрию выше ее симметрии в свободном состоянии;

группа позиционной симметрии должна быть одновременно подгруппой группы симметрии кристалла и свободной молекулы (иона) (рис. 2.11)

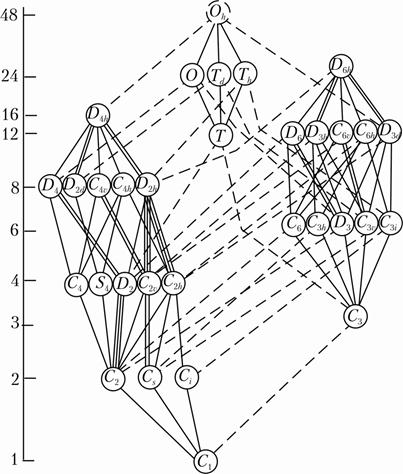
Рис.2.11 Соотношения между группами и подгруппами 32 кристаллографических точечных групп.

В общем случае симметрия молекулы (иона) понижается. Может случиться, что некоторые элементы симметрии сохранятся и станут общими, и для молекулы (иона), и для ее кристаллического окружения.

В этом случае центр масс молекулы (иона) будет располагаться в точке элементарной ячейки, которую называют позицией (частным положением). Эта позиция (точка) должна быть инвариантной (неизменной) относительно некоторых операций симметрии пространственной группы. Совокупность таких операций симметрии образует позиционную (точечную) группу симметрии, которую называют также сайт-группой

Пользуясь тем, что число, симметрия и кратность возможных наборов частных положений (позиций) всех 230 пространственных групп известны, нетрудно определить позиционную симметрию любой молекулы (иона) в кристалле.

Дата добавления: 2014-01-05