Основные характеристики комплексных соединений

РЕАКЦИИ КОМПЛЕКСООБРАЗОВАНИЯ

Лекция 6

Представление деревьев

Примеры деревьев

Степень вершины – число ее сыновей. Вершины без сыновей называют терминальными или листьями. Дуги называют ветвями.

Деревья

Пример.

Введите число вершин: 4

Введите номера смежных вершин

0: 1 3 -1

1: 0 2 3 -1

2: 1 -1

3: 0 1 -1

/* Функция ввода графа и формирования векторов смежности */

void VectSm (int vsm[NMAX][NMAX+1], int *pn)

/* Вых. данные: vsm – векторы смежности,

*pn – число вершин графа */

{ int i, j; /* номера вершин */

printf (“Введите число вершин:”);

scanf(“%d”, pn);

puts (“Введите номера смежных вершин”);

for (i = 0; i < *pn; i++)

{ printf (“%d: ”, i);

j = -1;

do scanf(“%d”, &vsm[i][++j]);

while (vsm[i][j]!= -1);

}

}

/* Вызов функции */

int vsm[NMAX][ NMAX+1]; /* векторы смежности */

int n; /* число вершин */

VectSm (vsm, &n);

В результате выполнения функции получится матрица:

| 0 1 2 3 4

------------------

0 | 1 3 -1

vsm = 1 | 0 2 3 -1

2 | 1 -1

3 | 0 1 -1

• 6. Списки смежности.

Для каждой вершины хранится список смежных с ней вершин.

Описание на языке С:

#define NMAX 10 /* макс. число вершин */

/* тип элемента списка */

struct LIST

{ int v; /* вершина */

struct LIST *next; /* ссылка на следующий элемент */

};

struct LIST *p [NMAX]; /* массив указателей списков смежности */

int n; /* число вершин */

Дерево – это связный неориентированный граф без циклов.

Связным называют граф, в котором для любых двух вершин существует связывающий их путь. Дерево из n вершин имеет n-1 ребер.

Дерево с одной выделенной вершиной называют корневым, а выделенную вершину – корнем дерева.

Корневое дерево обычно рассматривают как ориентированное от корня (реже к корню), но изображают без стрелок.

Уровень вершины определяется расстоянием вершины от корня.

Высота дерева – это максимальный уровень его вершин.

Преемников вершины называют сыновьями, а предшественника – родителем или отцом.

1. Структура организации и ее подразделений.

2. Родословное дерево.

3. Структура книги, состоящей из разделов и подразделов.

4. Структура сложной программы, где корень дерева – главная функция, вершины 1-го уровня – подпрограммы, вызываемые из главной функции и т.д.

Дерево называется упорядоченным, если сыновья каждой вершины упорядочены каким-либо образом.

Бинарное (двоичное) дерево – упорядоченное дерево степени 2: каждая вершина имеет не более 2-х сыновей, образующих корни ее левого и правого поддерева.

Деревья чаще всего хранят в виде сетей или списковых структур.

Каждый элемент сети содержит номер или метку вершины и указатели на элементы-сыновья.

В регулярной (однородной) сети число указателей у элементов одинаковое, а в нерегулярной сети – разное.

Комплексные соединения состоят из центрального иона (атома) М и окружающих его лигандов L. Сложность строения и своеобразие физико-химических и других свойств этих соедине­ний привели к появлению многочисленных определений самого понятия комплексное или координационное соединение. Однако общепринятого, достаточно совершенного определения создать пока не удалось. Под комплексными соединениями будем иметь в виду частицу, образованную двумя или большим числом частиц, способных к самостоятельному существованию в раство­ре (одной из частиц является ион металла). Несовершенства приведенного определения очевидны, однако оно отражает одну из наиболее характерных особенностей этой группы соединений.

Важной характеристикой координационного соединения явля­ется координационное число, показывающее число атомов или атомных группировок, непосредственно связанных с центральным ионом. Наиболее часто встречаются координационные числа шесть и четыре, реже — два. Менее известны соединения с коор­динационными числами три и пять, а также с более высоким, чем шесть.

Лиганды характеризуются дентатностью (от лат. dentatus — зубчатый), т. е. способностью занимать определенное число ко­ординационных мест около центрального иона. Моно- или однодентатные лиганды занимают одно координационное место, би- или двудентатные — два. Существуют пяти- и шестидентатные лиганды и лиганды с еще более высокой дентатностью, которая не всегда реализуется в связи с ограниченной координационной емкостью центрального иона. Полидентатные лиганды при реак­ции с ионом металла обычно образуют координационные соеди­нения, содержащие цикл — замкнутую группировку атомов. В простейшем случае, например, в результате реакции

Cu ²⁺ + NH₂CH₂COO^- = CuNH₂CH₂COO⁺

образующееся соединение содержит один пятичленный цикл

Нередко в молекуле координационного соединения насчитывается два, три и большее число циклов. Увеличе­ние прочности координационных соединений, содержащих пяти или шестичленные циклы, было замечено еще Л. А. Чугаевым и обобщено им в известном правиле циклов. Впослед­ствии координационные соединения с одним или несколькими циклами стали называть хелатными (от англ. chelate — клешня) или просто хелатами. В этой терминологии нашла отра­жение несложная аналогия полидентатного лиганда с клешней, прочно захватывающей ион металла при образовании координа­ционного соединения. Типичными хелатами являются соединения ионов металлов с комплексонами, имеющие большое значение в современной аналитической химии.

Комплексонами называют группу полиаминополикарбоновых кислот, простейшим представителем которой является

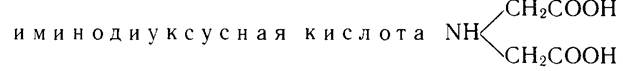
В водном растворе она имеет бетаиновую структуру, т. е. существует в виде биполярного, так называемого цвиттер-иона, несущего противоположные заряды:

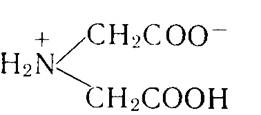
В кислом растворе карбоксильная группа также протонируется и биполярный цвиттер-ион превращается в обычный однозарядный ион

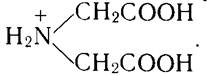
Широко известным представителем комплексов является этилендиаминтетрауксусная кислота ЭДТА, или комплексен II:

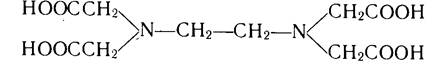
Как и иминодиуксусная, она существует в растворе в виде цвиттер-иона,

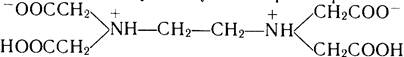
который при подкислении переходит в шестиосновный катион кислоты:

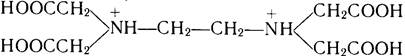
Двунатриевая соль ЭДТА известна также под названием комплексон III или трилона Б и др.

Известны также комплексоны, со­держащие гетероатомы (серу, кислород и др.) и кроме карбо­ксильной другие кислотные группы — алкилфосфоновую, алкиларсоновую, оксигруппу и т. п.

Значение комплексонов очень велико. Появление комплексо­нов открыло широкие перспективы и многообразные возмож­ности применения их в аналитической химии. Были разработаны новые методики анализа и найдены простые решения многих сложных аналитических проблем. С помощью комплексонов мо­жет быть определено более 60 элементов. Почти ни один раздел аналитической химии не обходится в настоящее время без при­менения комплексонов. Комплексоны эффективно применяют также во многих отраслях промышленности и быта.

Дата добавления: 2014-01-05