Summary of lecture № 7

TOPIC: STABILITY CRITERIA

1. STABILITY ANALYSIS WITH 1-st LYAPUNOV METHOD

The First Lyapunov method allows to judge about stability of the real system on roots of the characteristic equation of the linearized system:

.

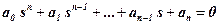If among the roots of the characteristic equation to find at least one has positive real part, that system is unstable.

If among the roots at least one will be zero root, the system can be both unstable and stable (not asymptotically).In this case, the stability is determined by the analysis of raw data (non-linear) equations of the system using the second method of Lyapunov.

The roots of the characteristic equation, presenting itself algebraic equation can be determined for the equations of the second, third and fourth powers of the coefficients by radicals. For determination the roots of the fifth, sixth, and other, more higher power there are approximate methods of calculation used (graphic, Horner's scheme, the method of polynomials dividing, buildings of Lilla, the method of Lagrange, method of Lobachevskii and others.).

Any algebraic equations of power at most 4, are solvable by radicals. Niels Henrik Abel, norwegian, in 1826 has proved that solving of the equation of 5 and greater powers is impossible. Evarist Galua, frenchman, in 1830 has got the full solution of the problem about that, under what conditions algebraic equation is solvable in radical.

Task 7.1. Examine stability of the closed-loop system of stabilization, which the characteristic equation has the form

.

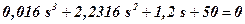2. STABILITY CRITERIA OF HURWITZ

Stability criterion of the German mathematician A. Hurwitz (1895) refers to algebraic stability criteria. The starting point for the criterion is the characteristic equation of linear control systems:

,

on the basis of which they composed the square matrix of Hurwitz – on the following rule:

- the size of a square matrix defined by the order n;

- the main diagonal of the matrix from the top left to bottom right are written, since the 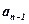coefficients of the characteristic equation;

- the column of the matrix are complemented coefficients with decreasing index up from the diagonal;

- the column of the matrix are complemented coefficients with increasing index down from the diagonal.

For the general form of the characteristic equation of the matrix can be represented as follows:

.

Task 7.2. The characteristic equation of the closed-loop system has the form

.

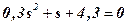Дата добавления: 2014-01-05