Please evaluate the stability of the system!

For research linear control systems higher-order possible to use the algebraic criterion Liénard-Shepherd: for stability of the linear system it is necessary and sufficiently that at positive coefficients of the characteristic equation, determinants of uneven order of the matrix H were positive. Thus, the criterion of Lienard-Shepherd reduces by half the number of the conditions for determination of linear control system stability.

Hurwitz stability criterion allows determine conditions for finding the control system to the stability boundary. The system will be located at the boundary of stability, if the positivity of all 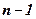determinants of the last determinant is equal zero:

.

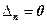From this condition following:

,

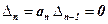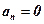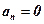is possible when or . Condition corresponds to an aperiodical stability boundary, and the condition the system is responsible for the oscillatory stability boundary.

3. 3. STABILITY CRITERIA OF NYQUIST

In 1932 american scientist Nyquist has offered the criterion of the study to stability of the amplifiers with single negative feedback. Nyquist criterion uses Nyquist diagram of open-loop system, on nature of which on complex plane judge about nature of stability of the closed system.

Nyquist criterion advantage compared with other criteria is that Nyquist diagram of open-loop system can be obtained as experimentally and analytically.

Nyquist criterion is formulated as follows:

On these figures there are examples of hodographs for different, for most typical cases.

In the fig. a shows the hodograph 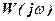of the open-loop system, which has two roots in the right half plane. Hodograph covers twice point 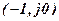, in the negativ direction, therefore, system in the closed-loop state is unstable, Nyquist diagram to open-loop system in the fig. b covers once point with coordinates 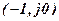in the positive direction, so the system in closed-loop state is stable. Nyquist diagram of the open-loop stable system in fig. c does not covers a point with coordinates 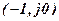, that testifies to stability of the system in the closed-loop state.

A particular case of the Nyquist stability criterion is the case of a stable open-loop system, i. e. when 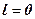. The criterion is formulated as follows:

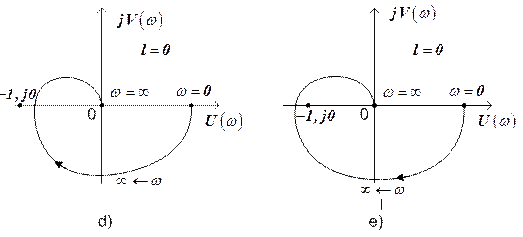
Examples of the stability of different control systems are shown in figures. On the fig. d Nyquist diagram of the open-loop system does not cover the point 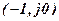, that testifies to stability of the system in closed state. Nyquist diagram in the fig. e covers the point 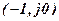, therefore the system in closed state is not stable.

Task 7.3 Determine the stability of the closed-loop system stabilize the angular velocity of the motor with open loop transfer function, which describes the processes near the working point:

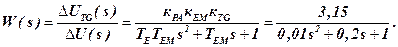
Here: 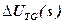– image on Laplace increment of the output voltage of the tachogenerator; 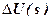– image on Laplace increment of the input voltage; 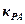– the coefficient of the power amplifier; 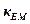– the coefficient transformation of the electric motor; 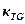– the coefficient transformation of the tachogenerator; – electromagnetic and 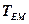– electromechanical time constants of the electric motor.

The characteristic equation of the open-loop system

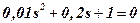
will have two real negative roots:

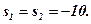
Consequently, the open-loop system is stable and therefore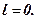

To construct the Nyquist diagram of the open-loop system define the real – and imaginary – characteristics:

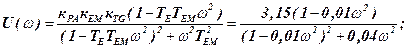
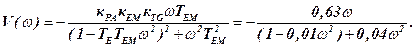
The results of calculations of the real and imaginary characteristics are shown in table. 7.1.

Table 7.1

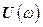
	3,15	2,49	1,51		-0,37	0,38	-0,25	-0,16
		-1,16	-2,01	-1,57	-0,89	-0,5	-0,19	-0,002

The resulting data allow us to construct Nyquist diagram of the open-loop system (fig. f). According to the Nyquist stability criterion for stable open-loop system hodograph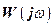should not cover the point with coordinates 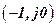. Built hodograph does not cover the point 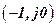, therefore, the stabilization system of angular velocity of the electric motor in the closed-loop state will be stable.

Nyquist criterion was also spread in determining the stability of control systems by a logarithmic frequency characteristics. Nyquist diagram of the open-loop system can be represented in the form:

,

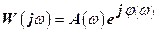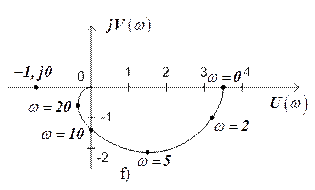thus it is completely determined by a pair of these characteristics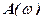and or similar characteristics

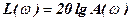и .

Obviously, the points of intersection locus 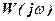with segment of negative real axis correspond the points for which 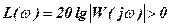, 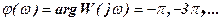. The point of intersection of the characteristic with straight line from the bottom up, called negative transitions, and top-down - positive transition logarithmic phase frequency characteristic. Then the Nyquist criterion of stability is formulated as follows:

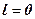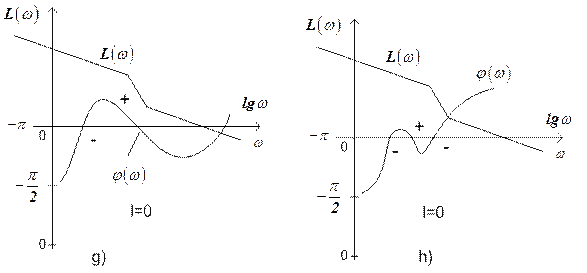
In the particular case, when (the system is stable or neutral in open-loop state), closed-loop system will be stable, if at 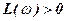the difference between positive and negative transitions is equal zero. In the fig. g and fig. h the characteristic arrangement of logarithmic characteristics of stable and unstable systems in the closed-loop state is shown.

Task 7.4 We define the stability of the closed-loop system of stabilization of the electric motor angular velocity (Task 7.3) with logarithmic Nyquist criterion.

Of solutions the characteristic equation of the closed-loop system follows, that , i.е. the number of roots in the right half plane 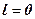. For constructing logarithmic frequency characteristic we represent transfer function of the open-loop system in that form:

.

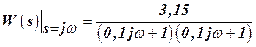The frequency of conjugation 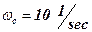. Point of intersection with the ordinate axis is defined as follows: .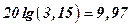

Phase frequency response of the system built on the basis of the equation:

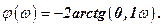
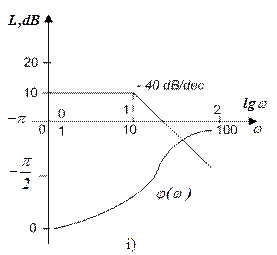
The build of the logarithmic characteristic is shown in fig. i. The figure shows that the phase frequency response does not cross the value , therefore, according to a logarithmic criterion, closed-loop system of stabilization will be stable.

Academician V. A. Steklov about A. M. Lyapunov

:

«He devoted all his exceptional power to selfless serving to science, he lived for science only, he saw sense of life in science only and often spoke that without scientific creative activity life itself costs nothing for him»

Дата добавления: 2014-01-05