Ионная сила раствора

Понятие ионной силы раствора I было введено в теорию электролитов Льюисом (1921). Под ней понимают полусумму произведений ионных концентраций в растворе на квадрат их валентности:

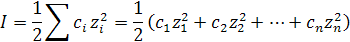
(9.10)

где С – концентрация ионов, моль/л.

Вычислим ионную силу 0,01 М растворов NaCI, KNO₃, CuSO₄, и AI₂(SO₄)₃:

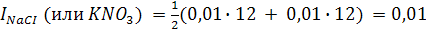
а ионная сила 0,01 М раствора AI₂(SO₄)₃, диссоциирующего по уравнению

AI₂(SO₄)₃ ↔ 2AI³⁺+ 3SO₄^2-

равна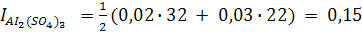

Итак, в растворах равных концентрации 1-1-валентных электролитов ионная сила одинакова. В растворах равных концентраций 1-1-валентных и 2-2-валентных электролитов число ионов, образующихся при диссоциации, одинаково. Однако ионная сила раствора СuSO₄ в 4 раза больше ионной силы раствора NaCI (КNO₃) вследствие того, что электростатическое взаимодействие между двухвалентными ионами сильнее, чем между одновалентными. Ионная сила раствора характеризует межионное взаимодействие. При одинаковой концентрации растворы многовалентных электролитов обладают большей ионной силой, т.е. ведут себя как более концентрированные растворы, так IАI₂(SO₄)₃ в 15 раз больше I_NaCI.Ионная сила 0,4М раствора Na₂SO₄ подкисленного серной кислотой (С=0,01 моль/л) равна:

При вычислении ионной силы необходимо пользоваться истинной ионной концентрацией; для слабого электролита эта величина равна

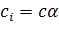(9.11)

где с – концентрация электролита, моль/л;

α – степень диссоциации электролита.

Средний коэффициент активности электролита можно рассчитать теоретически из предельного закона Дебая-Хюккеля (ПЗДГ):

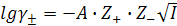(9.12)

где А – константа, для водных растворов при 25 ºС равна +0,51;

Z₊ и Z_– – валентность ионов;

I – ионная сила раствора.

Из ПЗДГ следует, что ионная сила влияет на коэффициент активности: во всех разбавленных растворах с одинаковой ионной силой (I ≤ 0,02) коэффициент активности сильного электролита одинаков, независимо от природы электролитов, присутствующих в растворе (закон ионной силы). ПЗДГ применим только для разбавленных растворов электролитов с ионами низкой валентности. Из закона следует, что с уменьшением ионной силы раствора коэффициент активности увеличивается.

Согласно ПЗДГ, коэффициенты активности ионов Na ⁺ и 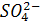в 0,001М растворе Na₂SO₄ при 25ºС (I = 0,3∙10^–2):

откуда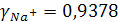

откуда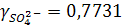

Средний коэффициент активности, определяемый уравнением (9.9):

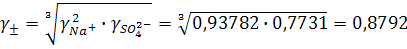
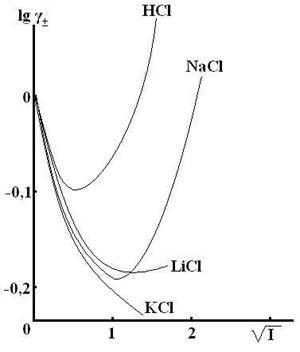
Рис. 9.1 Зависимость lg γ_± от 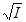, рассчитанная по уравнению Дебая-Хюккеля.

Коэффициент активности для разбавленного раствора сильного
электролита представляет собой поправку к концентрации, обусловленную главным образом электростатическим взаимодействием ионов, которое определяется зарядами и радиусами ионов и не зависит от химической природы электролита.

Следует предположить, что если катион и анион электролита имеют одинаковые по величине заряды и близкие радиусы, т.е. элетростатически равноценны, то коэффициенты активности таких ионов одинаковы. Такими электролитами являются соли типа КСI, КF, СsI. Экспериментально для 0,01 М раствора КСI найдено, что γ_± равен 0,922, следовательно, в растворе этого электролита

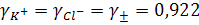
Коэффициент активности, а значит, и сама активность определенного иона, например катиона К⁺, зависит от активности аниона, так, например, в 0,01 М растворе сульфата калия 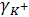будет иным, чем в 0,01 М растворе хлорида калия.

В дальнейшем под термином „коэффициент активности” мы будем понимать средний коэффициент активности, определяемый опытным путем или рассчитываемый по ПЗДГ. Экспериментальные исследования показали, что величина коэффициентов активности ионов в растворе зависит от Z (зарядов) и с (концентрации) всех ионов. Понятие об ионной силе раствора впервые ввел Льюис (1921). Согласно определению, ионная сила раствора равна полусумме произведений концентраций ионов на квадрат их заряда

(9.13)

Пример: в 1000 г. воды растворены 0,01 моль K₂SO₄ и 0,1 моль MgCI₂. Определить ионную силу раствора.

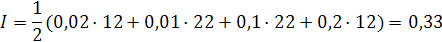
Приближенное значение I природных вод рассчитывается по формуле:

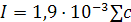, (9.13а)

где C – общая минерализация раствора, мг/л.

Льюис и Рендал также установили закон ионной силы, который гласит, что коэффициенты активности электролита (ионов) зависят от ионной силы, но не зависят от вида остальных ионов в растворе. Закон выполняется до величины ионной силы порядка пяти-шести сотых долей единицы.

9.4 Теория растворов сильных электролитов Дебая-Хюккеля.

Согласно современной теории растворов электролитов, основные положения которой сформулированы Дебаем и Хюккелем (1923), сильные электролиты в растворах полностью диссоциируют на ионы. Теория Дебая-Хюккеля, поэтому иногда называется «теорией полной диссоциации».

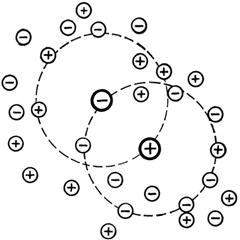
Однако в растворах в отличие от ионных кристаллов солей тепловое движение ионов приводит к тому, что они не сохраняют своего фиксированного положения, а располагаются вокруг выбранного центрального иона в виде шаровой сферы, которая называется ионной атмосферой. Все ионы, находящиеся в растворе, равноправны, каждый из них окружен ионной атмосферой и каждый из них может быть центральным.

Рис. 9.2 – Модель ионной атмосферы

Рассмотрим отрицательный ион в качестве центрального. Вокруг этого иона могут находиться как положительные, так и отрицательные ионы, последние вследствие электростатического отталкивания располагаются дальше от центрального иона. В целом ионная атмосфера имеет заряд, противоположный по знаку заряду центрального иона. Тепловое движение ионов в растворе приводит к тому, что они непрерывно обмениваются местами с ионами других ионных атмосфер. Однако вокруг отрицательно заряженного иона образуется ионная атмосфера, у которой преобладает положительный заряд, вокруг положительного – ионная атмосфера с отрицательным зарядом, но в целом весь раствор остается нейтральным. Плотность ионной атмосферы различна: чем разбавленнее раствор, тем плотность ее меньше, чем концентрированнее
раствор, тем плотность атмосферы больше и больше ее влияние на центральный ион, так как сильнее проявляется межионное электростатическое
взаимодействие. С повышением температуры плотность ионной атмосферы уменьшается за счёт увеличения кинетической энергии ионов. Электростатическое взаимодействие ионов в растворе сильно зависит и от диэлектрической постоянной растворителя: силы взаимодействия ионов увеличиваются при уменьшении электрической постоянной растворителя.

Однако как ни велики достижения теории Дебая-Хюккеля ее приложение ограничивается разбавленными растворами сильных электролитов с
ионами низкой валентности, так как она учитывает лишь эффект электростатического взаимодействия ионов, не принимая во внимание силы, действующие между ионами и молекулами растворителя (т.е. сольватацию ионов). Наконец, теория Дебая-Хюккеля не учитывает также индивидуальных свойств ионов, которые определяются их строением, поляризуемостью.

Дальнейшее развитие теории межионного взаимодействия сильных электролитов связано с распространением ее положений на более концентрированные растворы, учетом явлений сольватации ионов и их возможной ассоциации. Ряд авторов высказал предположение, что при значительных концентрациях электролитов в растворах может происходить ассоциация ионов, когда противоположно заряженные ионы сближаются, образуя ионные двойники, например К⁺ + СI^– = КСI. Ионные пары удерживаются вместе только за счет кулоновских сил, поэтому влияют друг на друга не так сильно, как при типичном образовании молекул. Степень ассоциации ионов была подсчитана и сопоставлена с экспериментальными данными. Результаты показали, что ионная ассоциация играет значительную роль, особенно в неводных растворителях с низкой диэлектрической постоянной. Свойства растворов электролитов определяются концентрацией ионов данного электролита в растворе.

Поведение ионов одного знака сильно зависит от наличия ионов противоположного знака, поэтому химическая активность иона i не соответствует его действительной аналитической концентрации в растворе, так как между ионами проявляется электростатическое взаимодействие. Для характеристики поведения реальных систем американским ученым Льюисом введено понятие активности, которое широко используется, особенно в применении к растворам сильных электролитов.

Основой современных теорий сильных электролитов является теория Дебая и Хюккеля (1923). При разработке теории авторы исходили из следующих основных положений:

1. Электролиты в растворе полностью диссоциируют на ионы.

2. Все отклонения активности (а) от концентрации (с) обусловлены только кулоновскими силами взаимодействия между ионами.

3. Дебай и Хюккель ввели представление об ионной атмосфере в растворе электролита.

4. Авторы теории пренебрегали собственными размерами ионов, считая их точечными зарядами.

Расчет коэффициента активности ионов может быть произведен только на основании теоретических рассуждений. Например, исходя из предельного закона Дебая-Хюккеля, согласно которому коэффициент активности данного иона (катиона или аниона) в разбавленных растворах сильных электролитов определяется его зарядом и общей ионной силой раствора.

На основе изложенных положений было предложено уравнение первого приближения закона Дебая-Хюккеля, которое имеет следующий вид:

а) 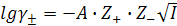(9.14)

где А – константа (+0,51),

Z₊ и Z_– – заряды ионов,

I – ионная сила раствора.

б) уравнение второго приближения закона Дебая-Хюккеля расширяет концентрационные пределы теории и учитывает размеры ионов:

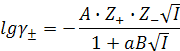
(9.15)

где α = 3÷6 · 10^{-8 см = 3÷6Å}

В – константа, при обычных условиях равна 0,328. Для 1-1-валентных электролитов, 1-2-валентных электролитов применимо для растворов с ионной силой порядка нескольких десятых долей единицы.

в) уравнение третьего приближения включает дополнительно слагаемое сI, где с – подбираемые параметр для полного согласования расчетных и экспериментальных данных:

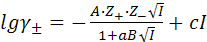(9.16)

Рядом авторов были предложены различные эмпирические формы вышеприведенных уравнений:

1) Уравнение Гюнтельберга (1926)

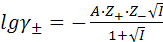(9.17)

при а = 3,04Ǻ, Т= 298К

2) Формула Гуггенгейма

(9.18)

где В – некоторая постоянная величина,

с – молярная концентрация электролита.

3) Уравнение Дэвиса

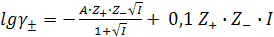(9.19)

Это наиболее удобное уравнение, которое хорошо описывает экспериментальные данные до 0,2М растворов для любого зарядного типа электролита, кроме раствора AI₂(SO₄)₃.

Робинсон и Стокс получили хорошие результаты совпадения расчетных и экспериментальных данных γ_± для концентрированных растворов (до концентрации 4М) применив уравнение:

(9.20)

где h – количество молекул Н₂О, связанных с 1 молекулой растворенного вещества;

ν – число ионов, получающихся при распаде одной молекулы электрол та на ионы;

– активность воды;

m – моляльность раствора.

В уравнении Робинсона-Стокса первое слагаемое – отрицательная величина, введённая Дебаем-Хюккелем; второе слагаемое – поправка на пониженную активность воды в солевом растворе, положительная величина, т.к. < 1; третье слагаемое учитывает гидратацию ионов, т.е. связывание ν
ионов с h молекулами воды, которые перестают действовать как молекулы растворителя. Может быть положительной, равной 0 или отрицательной величиной, когда h > 0, h = 0, h < 0.

Схема расчета показателей активности ионов (pKat, pAn)

а) определение концентрации катионов и анионов в растворе;

б) расчёт величины I по результатам катионно-анионного состава раствора электролита;

в) расчёт значения среднего ионного коэффициента активности 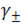по вышеприведённым уравнениям;

г) расчёт средней ионной активности а_± = γ_± · с;

д) pKаt = – lg a_Kat; pAn = – lg a_An

Дата добавления: 2014-01-05