Характеристики положення

Анализ целостности сигнала и взаимовлияния компонентов платы

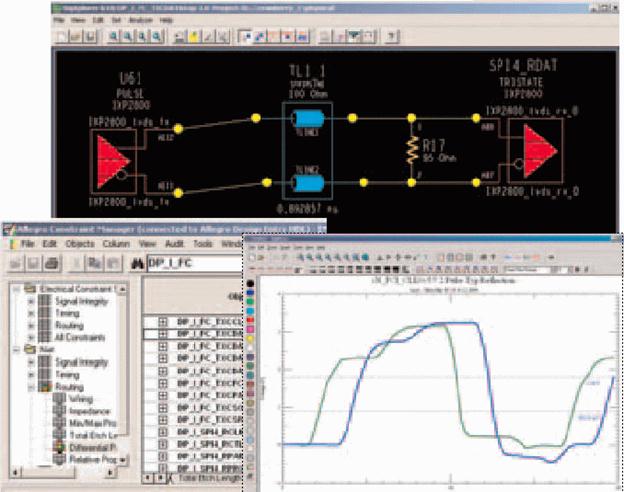
http://khpi-iip.mipk.kharkiv.edu/library/sapr/lab/lb01.html http://kiryushin.boom.ru/uts/p1-2125.htm

а) Математичне сподівання випадкової величини

Однією з найчастіше застосовуваних на практиці характеристик є математичне сподівання. Термін «математичне сподівання» випадкової величини є синонімом терміна «середнє значення» випадкової величини.

Означення . Математичним сподіванням дискретної випадкової величини, яка набуває значень із скінченної множини чисел, називається число

, (5)

яке дорівнює сумі добутків значень випадкової величини на відповідні ймовірності.

Означення. Математичним сподіванням неперервної випадкової величини, яка має щільність розподілу, називається число

(6)

Властивості математичного сподівання

1. Математичне сподівання сталої величини С дорівнює самій сталій:

.

Справді, сталу можна розглядати як випадкову величину, що з ймовірністю, яка дорівнює одиниці, набуває значення, а тому.

2. Сталий множник можна виносити за знак математичного сподівання:

3. Математичне сподівання суми двох випадкових величин дорівнює сумі математичних сподівань цих величин, тобто

Ця властивість виконується і для будь-якого скінченого числа випадкових величин.

4. Якщо дві випадкові величини незалежні, то математичне сподівання їх добутку дорівнює добутку математичних сподівань цих величин, тобто

Ця властивість виконується і для будь-якого скінченого числа незалежних випадкових величин.

Якщо випадкова величина, то, а саме: математичне сподівання випадкової величини має обов’язково міститися всередині інтервалу, являючи собою центр розподілу цієї величини.

Приклад 5. Закон розподілу дискретної випадкової величини задано таблицею (приклад 1):

	–4	–1
	0,1	0,2	0,1	0,3	0,1	0,2

Обчислити.

Розв’язання: За формулою (1)

.

Приклад 6. За заданою щільністю ймовірностей (приклад 2)

знайти.

Розв’язання. За формулою (2)

.

б) Мода та медіана випадкової величини

Означення. Модою () дискретної випадкової величини називається те її можливе значення, якому відповідає найбільша ймовірність.

Якщо випадкова величина має одну моду, то такий розподіл ймовірностей називають одномодальним; якщо розподіл має дві моди — двомодальним і т. ін. Існують і такі розподіли, які не мають моди. Їх називають антимодальними.

Приклад 7. Для дискретної випадкової величини з прикладу 1.

Означення. Модою неперервної випадкової величини Х називаються те її можливе значення, якому відповідає максимальне значення щільності ймовірності:

. (7)

Означення. Медіаною () випадкової величини називається те її значення, для якого функція розподілу задовольняє умові

(8)

Приклад 8. Для неперервної випадкової величини з прикладу 2 питання 5, заданої щільністю ймовірностей

знайти,.

Розв’язання. Графік щільності зображено на малюнку:

Згідно з графіком маємо. Отже,.

Визначимо. Для цього знайдемо функцію розподілу:

Отже,

Для визначення застосовуємо рівняння (3):

можна також знайти, скориставшись щільністю ймовірностей:

,

або при:

.

Отже, — таке можливе значення випадкової величини, що пряма, проведена перпендикулярно до відповідної точки осі на площині, поділяє площу фігури, яка обмежена функцією на дві рівні частини.

2) Характеристики розсіювання:

Дисперсія та середнє квадратичне відхилення

Різні випадкові величини можуть мати одне й те саме математичне сподівання, але істотно різний характер розподілу.

Тому необхідно ввести ще одну числову характеристику випадкової величини – для виміру ступеня розсіювання, розкиду значень випадкової величини навколо її математичного сподівання. Тому математичне сподівання називають ще центром розсіювання. Для вимірювання розсіювання вводиться числова характеристика, яку називають дисперсією.

Означення. Дисперсією випадкової величини Х називається математичне сподівання квадрата відхилення цієї випадкової величини від її математичного сподівання:

(9)

Очевидно, чим менше дисперсія випадкової величини Х, тим краще значення випадкової величини описуються її математичним сподіванням.

На практиці для обчислення дисперсії застосовується так звана робоча формула:

(10)

Для дискретної випадкової величини

(11)

Для неперервної випадкової величини

. (12)

Слід пам’ятати, що дисперсія не може бути від’ємною величиною.

Властивості дисперсії

1. Дисперсія сталої величини дорівнює нулю:

Справді,.

2. Сталий множник можна виносити за знак дисперсії, підносячи до квадрату:

.

Маємо:

.

3. Якщо дві випадкові величини незалежні, то дисперсія їх суми або різниці дорівнює сумі дисперсій цих величин, тобто

Ця властивість виконується і для будь-якого скінченого числа випадкових величин.

Отже, дисперсія характеризує розсіювання випадкової величини відносно свого математичного сподівання. Якщо випадкова величина виміряна в деяких одиницях, то дисперсія вимірюватиметься в цих самих одиницях, але в квадраті.

Тому доцільно мати числову характеристику такої самої вимірності, як і випадкова величина. Такою числовою характеристикою є середнє квадратичне відхилення.

Означення. Середнім квадратичним відхиленням випадкової величини Х називається корінь квадратний з дисперсії:

.

Приклад 9. Для дискретної випадкової величини з прикладу 1.

	–4	–1
	0,1	0,2	0,1	0,3	0,1	0,2

обчислити,.

Розв’язання. За формулою (4) маємо:

.

Знайдемо:.

.

Тоді

;

Приклад 10. Для неперервної випадкової величини з прикладу 2, заданої щільністю ймовірностей

обчислити,.

Розв’язання. Знайдемо;

.

За формулою (4)

;

Дата добавления: 2014-01-05