Номинальная шкала

Зависимость применимости метода прогнозирования от шкалы

Графическое представление вариационных рядов

Тема 2. Корреляционные методы

Прогнозирование средствами мат. статистики производится на основе анализа вариационных рядов и их связей.

Варьирование - изменение признака от наблюдения к наблюдению. (Например, варьирование веса или роста в к.-л. группе людей).

Вариационный ряд – количественная характеристика варьирования признака.

Прогнозирование представляет собой суждение на основе знания:

- совместного изменения двух (или более) признаков в ряде наблюдений

- известного значения одного признака (фактора) (или более) в новом наблюдении

о наиболее вероятном значении второго признака.

Фактор[ы] – признак[и] на основе которого производится предсказание значения другого признака - регрессии.

Для выработки такого суждения необходимо:

- описать закономерность связи между регрессией и факторами (в виде: математической функции; перечисления или алгоритма)

- оценить силу этой закономерности - степень зависимости между признаками (фактором и регрессией). Количественная оценка такой зависимости существенно определяется шкалой измерения признаков.

Количество может быть измерено в различных шкалах.

Шкала	Допустимая операция	Пример
Номинальная	=	Имена
Порядковая	= <>	Баллы
Разностная	= <> + -	Температура, Прибыль
Абсолютная	= <> + - * /	Вес, Выручка

Заключение о связи признаков можно получить графическим (зрительным / визуальным) и расчётным (аналитическим) путём. Взаимосвязь признаков номинальной шкалы отображается Пузырьковой диаграммой. Из двух признаков один рассматривается как независимый (фактор) – ось абсцисс(X), а другой как определяемый им (зависимый) – ось ординат(Y). Деление признаков на «независимый» и «зависимый» зависит от исследователя.

Рисунок 1‑1 Пузырьковые диаграммы признаков «Район» и «Орг.-правовая форма»

Для ответа на вопрос есть ли связь между признаками, нужно сопоставить диаграммы с крайними случаями, когда признаки независимы или зависимы полностью.

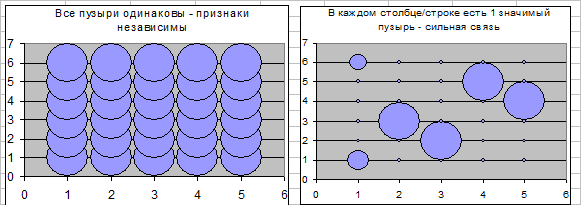
Рисунок 1‑2 Предельные случаи Пузырьковой диаграммы

Из примера видно, что зависимость одного признака от второго и обратная зависимость второго от первого просматриваются различным образом. Количественная мера близости для номинальной шкалы – условная энтропия (см. курс «ТХС») отражает это: .

Прогнозом является суждение о том, что если у нового объекта известно значение одного признака (фактора), то значение другого признака он принимает с определённой вероятностью. Например, если фирма Приморского района (3), то это скорее всего ООО (1) и вряд ли АООТ(5). Если же фирма – ИЧП, то, почти наверняка из Приморского р-на.

Дата добавления: 2014-01-05