Меры близости рядов

Вопросы на 5

Достоинства и недостатки метода

???

Какое понятие включает в себя другое: тренд или сглаженный ряд?

Каков порядок проведения медианного сглаживания?

Какое сглаживание целесообразно производить первым – экспоненциальное или скользящим средним?

Тема 7. Расчёт параметров уравнения тренда

После того, как определён тип тренда, необходимо рассчитать его параметры. Т.е. из всех возможных линий данного типа выбрать наиболее похожую на исходный ряд. Существенную роль играет конкретизация «похожести» (критерий меры близости рядов). В зависимости от критерия находятся методы расчета параметров.

Иногда, для различных участков ряда строят свои тренды. Их согласование приводит к построению сплайн-функций.

После того как определён вид уравнения тренда, необходимо определить (провести, построить) сам тренд, т.е. - определить его параметры. Из бесконечного множества трендов [определённого ранее вида] нужно выбрать тренд наипохожий на исходный ряд. Критерий выбора – минимизация расхождений [значений тренда и ряда]. Однако, что считать мерой близости (= расхождения)?.

Близость тренда к ряду в каждый из моментов времени можно оценить разницей значений в этот момент (чем меньше, тем лучше): 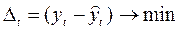. Но как оценить близость в целом (по всем наблюдениям) [на основе близости в каждый момент]?

Существует множество подходов в рамках т.н. «функций коллективного выбора» (см. Мулен Э. Кооперативное принятие решений), рассмотрим простейшие.

Оценка в целом (мера) близости может быть построена как:

максимум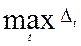
сумма	расхождений по всем наблюдениям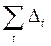
произведение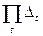

При этом следует учитывать, что отклонение тренда от ряда в одну сторону, может компенсироваться удалением в другую сторону в другой момент. Для устранения этого в функции меры можно использовать вместо 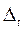также модуль и квадрат:.

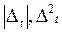Из полученных 9 вариантов меры, применительно к критерию на min, здравы лишь 4 (а то и 2):

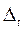
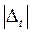
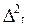
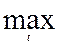
	Бессмысленно (тренд уходит вниз).	Неоднозначность решения
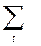
	Неоднозначность решения	Наиболее распространён
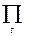
	Бессмысленно из-за множественности решений. Минимум (0) достигается любым трендом, совпадающим с рядом хотя бы в один момент.

(Меры на основе произведения применимы, если в качестве отклонения в момент времени принять не разницу 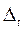, а отношение ).

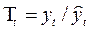Рисунок 1‑12 демонстрирует, что [линейный] тренд можно построить по-разному. При этом тренд, параметры которого рассчитаны на основе минимизации максимального модуля, даёт особо отличный результат (расчет произведён методом математического программирования).

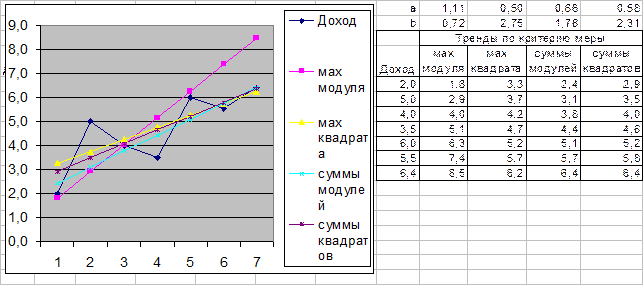
Рисунок 1‑12 Влияние меры близости рядов на построение тренда

Т.о., результат прогнозирования существенно зависит от выбранной меры.

Меры на основе суммирования можно усовершенствовать, введя взвешивание. Вполне логично предположить, что более поздние наблюдения имеют для прогнозирования большее значение.

Дата добавления: 2014-01-05