
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Некоторые характеристики САУ
|
|
|
|
Системы непрерывного и дискретного действия
Системы стационарные и нестационарные
Стационарной называется система, все параметры которой не изменяются во времени. Нестационарная система — это система с переменными параметрами или даже структурой. При математическом описании нестационарной системы это проявляется в том, что некоторые коэффициенты описывающего ее дифференциального уравнения являются функциями времени. Пример нестационарной системы — система управления ракетой, масса которой изменяется вследствие расхода топлива.
В соответствии с данным определением, в отличие от нестационарной системы, реакции стационарной системы на одно и то же воздействие не зависит от момента времени приложения этого воздействия.
САУ бывают непрерывного или дискретного действия в зависимости от характера действия составляющих систему звеньев.
Система непрерывного действия или, короче, непрерывная система состоит только из звеньев непрерывного действия, т. е. звеньев, выходная величина которых изменяется плавно и непрерывно при плавном изменении входной величины.
Система дискретного действия или дискретная система — это система, содержащая хотя бы одно звено дискретного действия. Звеном дискретного действия называется звено, выходная величина которого изменяется дискретно, т. е. скачками, даже при плавном изменении входной величины. (Скачки выходной величины могут происходить либо при прохождении входной величиной определенных пороговых значений — это звено релейного действия, либо в определенные моменты времени — звено импульсного действия.)
Устойчивость — это свойство системы возвращаться в установившееся состояние после того, как она была выведена из этого состояния каким-либо возмущением. Замкнутые САУ, как всякие замкнутые системы, весьма склонны к потере устойчивости, что чаще всего проявляется в возникновении расходящихся колебаний (генерации). Можно сказать, что устойчивость является необходимым условием работоспособности всякой САУ.
Качество процесса управления характеризуется тем, насколько процесс управления близок к желаемому. Количественно оно определяется показателями (критериями) качества, которые выбираются в соответствии с целью управления.
Важным показателем качества управления является точность управления. Например, для системы регулирования напряжения генератора точность определяется величиной установившегося отклонения напряжения генератора от заданного значения по окончании переходного процесса.
Идентификация объектов управления — это определение их математического описания — математической модели по экспериментальным данным их функционирования и априорным сведениям о таких объектах.
Наблюдаемость — это наличие допустимых измерению выходных координат вектора X, достаточных для определения текущего состояния объекта управления и, следовательно, для управления этим состоянием.
Управляемость — это наличие управляющих воздействий в векторе U, необходимых для осуществления такого управления.
|
Одномерная линейная непрерывная нестационарная система управления описывается дифференциальным уравнением
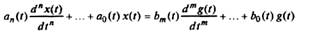 (1) (1)
|
с начальными условиями
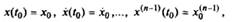 (2) (2)
|
где 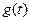 — входной сигнал;
— входной сигнал; 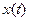 - выходной сигнал; — время;
- выходной сигнал; — время; 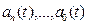 ,
, 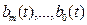 - коэффициенты левой и правой частей уравнения;
- коэффициенты левой и правой частей уравнения; 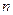 и
и  - порядки старших производных выходного и входного сигналов соответственно;
- порядки старших производных выходного и входного сигналов соответственно; 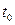 - момент начала функционирования системы.
- момент начала функционирования системы.
Если коэффициенты уравнения постоянны, система называется линейной стационарной.
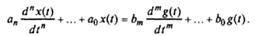 (3) (3)
|
В операторной форме уравнение (1) имеет вид
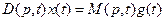 ,
,
где 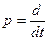 — символ, обозначающий операцию дифференцирования;
— символ, обозначающий операцию дифференцирования;  ,
, 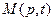 — дифференциальные операторы левой и правой частей уравнения (1.3):
— дифференциальные операторы левой и правой частей уравнения (1.3):
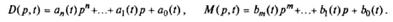
|
Уравнение (3) в операторной форме имеет вид
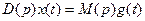 (4)
(4)
где
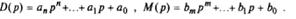
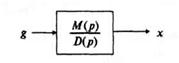
Из операторной формы уравнения следует способ изображения стационарной системы на структурных схемах (рис. 13.1).
|
Рис. 13.1
Сложные системы управления, как правило, состоят из элементарных и
типовых звеньев.
1. Усилительное звено описывается уравнением
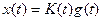 (5)
(5)
где 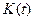 — коэффициент усиления. Если звено стационарное, то
— коэффициент усиления. Если звено стационарное, то  .
.
2. Дифференцирующее звено описывается уравнением
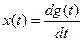 (6)
(6)
Выходной сигнал равен производной входного сигнала. Уравнение (6) в операторной форме имеет вид 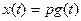
3. Интегрирующее звено описывается уравнением
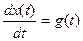 (6)
(6)
Выходной сигнал получается в результате интегрирования входного. В операторной форме уравнение (6) имеет вид  или
или 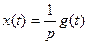 .
.
4. Звено чистого запаздывания описывается уравнением 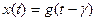 , где
, где 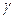 — величина запаздывания выходного сигнала относительно входного.
— величина запаздывания выходного сигнала относительно входного.
|
1. Построение структурной схемы по дифференциальному уравнению. Структурные схемы строятся с помощью элементарных, типовых звеньев и сумматоров, описывающих преобразование сигналов. Они служат одним из языков описания систем управления. По структурным схемам, как правило, находится эквивалентный оператор системы управления, а затем решаются различные задачи анализа.
АЛГОРИТМ ПОСТРОЕНИЯ СТРУКТУРНОЙ СХЕМЫ
1. Выразить член со старшей производной из дифференциального уравнения (1.3) и представить полученное соотношение с помощью сумматора, дифференцирующих и усилительных звеньев.
2. Все низшие производные получить как сигналы на соответствующих выходах последовательно соединенных интегрирующих звеньев.
3. Начальные условия (2) представить как постоянные во времени воздействия, приложенные на выходах интегрирующих звеньев.
Пример 1.1. Построить структурную схему системы, описываемой дифференциальным уравнением
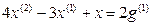
с начальными условиями 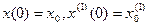 .
.
Выразим из уравнения член со старшей производной:
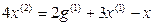
Изобразим схему получения сигнала 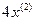 (рис. 13.2). С помощью усилительного звена с коэффициентом усиления 1/4 получим сигнал
(рис. 13.2). С помощью усилительного звена с коэффициентом усиления 1/4 получим сигнал 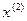 . Построим теперь прямую цепь схемы, последовательно преобразовывая сигнал
. Построим теперь прямую цепь схемы, последовательно преобразовывая сигнал 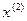 интегрирующими звеньями. Добавляя на выходах интегрирующих звеньев соответствующие начальные условия, получаем часть прямой цепи схемы, в которой присутствуют выходной сигнал х и его производные
интегрирующими звеньями. Добавляя на выходах интегрирующих звеньев соответствующие начальные условия, получаем часть прямой цепи схемы, в которой присутствуют выходной сигнал х и его производные 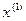 ,
, 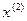 . Изображаем сумматор, выходным сигналом которого служит
. Изображаем сумматор, выходным сигналом которого служит 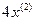 . На этом сумматоре нужно реализовать равенство
. На этом сумматоре нужно реализовать равенство 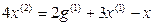 .
.
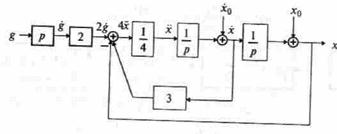
|
Рис. 13.2
Для этого добавляем к прямой цепи соединение дифференцирующего и усилительного звеньев, которые из входного сигнала 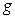 позволяют получить нужный сигнал
позволяют получить нужный сигнал  на входе сумматора. Сигналы
на входе сумматора. Сигналы 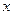 и
и 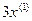 подаем на сумматор с соответствующим знаком, используя обратные связи. Таким образом, получаем структурную схему (рис. 13.2), соответствующую заданному дифференциальному уравнению.
подаем на сумматор с соответствующим знаком, используя обратные связи. Таким образом, получаем структурную схему (рис. 13.2), соответствующую заданному дифференциальному уравнению.
Пример 1.2. Построить структурную схему системы, описываемой дифференциальным уравнением
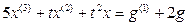
с начальными условиями 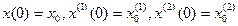 .
.
Выразим из уравнения член со старшей производной:
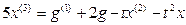
Согласно алгоритму получим структурную схему системы (рис. 13.3).
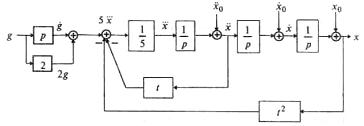 |
Рис. 13.3
Пример 1.3. Построить структурную схему системы, описываемой дифференциальным уравнением
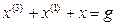
Выразим из уравнения член со старшей производной:
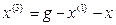
и с помощью алгоритма получим схему (рис. 13.4)
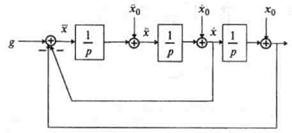 |
Рис. 13.4
2. Составление дифференциального уравнения по структурной схеме. Для записи дифференциального уравнения следует обозначить на схеме все промежуточные сигналы, записать уравнения для каждого звена и для каждого сумматора и из полученной системы дифференциальных и алгебраических уравнений исключить промежуточные переменные кроме входного и выходного сигналов.
Пример 1.4. Составить дифференциальное уравнение по структурной схеме, изображенной на рис. 13.5.
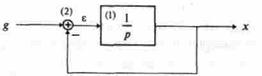 |
Рис. 13.5
Составим уравнения элементов схемы:
1) 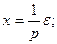 2)
2) 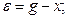
Отсюда
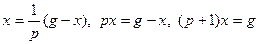
Дифференциальное уравнение системы имеет вид
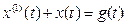 ,
,
Пример 1.5. Составить дифференциальное уравнение по структурной схеме, представленной на рис. 13.6.

|
Рис. 13.6
Составим уравнения элементов схемы:
1) 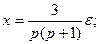 2)
2) 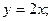 2)
2) 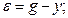
Отсюда
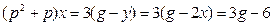
Переходя от операторной формы записи дифференциального уравнения к обычной, получаем
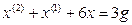
|
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 4339; Нарушение авторских прав?; Мы поможем в написании вашей работы!