Композиція відображень

Означення 3.8. Якщо f: A ® В, g: B ® C, то їх композиція (g ° f): A ® C, причому (g ° f)(а) = g (f (а)). Іншими словами, якщо існує множина пар (а,b)Î f та (b,c)Î g, то множина пар (а,с)Î f ° g утворює композицію (g ° f).Запис (g ° f) проводиться в порядку, який є зворотнім до того, в якому виконується операції f: A ® В, g: B ® C. Таким чином, в математиці прийнято правило, згідно з яким композицію відображень (g ° f) треба починати з виконання операції f, яка розташована справа.

Наприклад, якщо f = sin, g = ln, то (g ° f)(а) = (ln°sin)(a) = ln(sin(a)).

Легко показати, що композиція відображень асоціативна, тобто (h ° g)° f = h °(g ° f) і записується у вигляді h ° g ° f. Так само легко з’ясувати, що композиція відображень не комутативне (це випливає з означення композиції відображень).

Теорема 3.2. Функція f є взаємно однозначним функціональним відношенням тоді і тільки тоді, коли f ^–1 – взаємно однозначне відношення.

Доведення. Доведемо, що f ^–1 – функція. Нехай (b,a₁)Î f ^–1, (b,a₂)Î f ^–1. за означенням оберненого відношення маємо (a₁,b)Î f, (a₂,b)Î f. Оскільки f за умовою є взаємно однозначною функцією, дістанемо a₁ = a₂, а це означає, що f ^–1 – функціональне відношення. Покажемо, що f ^–1 – взаємно однозначне функціональне відношення. Нехай (b₁,a)Î f ^–1, (b₂,a)Î f ^–1. Це означає, що (a,b₁)Î f, (a,b₂)Î f. Оскільки f – функція, маємо b₁ = b₂, а це означає, що f ^–1 є взаємно однозначним функціональним відношенням. Таким чином, необхідну умову теореми доведено. Читачеві пропонуємо показати, що таким чином доведено також її достатню умову. ►

Теорема 3.3. Композиція двох функціональних відношень є функціональним відношенням.

Доведення. Нехай f: A ® В, g: B ® C. За означенням композиції відношень h = (g ° f) = {(a,c) | ((a,b)Î f та (b,c)Î g }. Отже, це за означенням – підмножина декартового добутку А´С. Доведемо, що h – функціональне відношення. Нехай задано дві пари, які належать h:

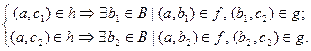
Оскільки f – функціональне відношення, маємо b₁=b₂, а оскільки g – функціональне відношення, дістаємо c₁=c₂. Отже h – функціональне відношення. ►

Теорема 3.4 (без доведення). Нехай f: A ® В, g: B ® C. Тоді

а) якщо f і g – сюр’єкції А на В та В на С відповідно, то g ° f є сюр’єкцією А на С. Іншими словами, композиція двох сюр’єкцій – сюр’єкція.

б) якщо f і g – ін’єкції, то g ° f є ін’єкцією. Іншими словами, композиція двох ін’єкцій – ін’єкція.

в) якщо f і g – бі’єкції, то g ° f є бі’єкцією. Іншими словами, композиція двох бі’єкцій – бі’єкція.

Для багатомісних функції f: A^m ® В, g: Bⁿ ® C можливими є різні варіанти підстановки f у g, які дають функції різних типів. Наприклад, при m=3, n=4 функція h ₁= g (b₁, f (a₁,a₂,a₃),b₃,b₄) має шість аргументів і діє з B´A³´B²®C, а функція h ₁= g (f (a₁,a₂,a₃), f (d₁,d₂,d₃),b₃,b₄) має вісім аргументів та діє з A⁶´B²®C. Особливо цікавим є випадок, коли задано множину функцій типу f_i: 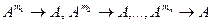. У цьому разі може виконане будь-яке перейменування аргументів, наприклад, перейменування a₃ в a₂, що породжує з функції f (a₁,a₂,a₃,a₄) функцію трьох аргументів f (a₁,a₂,a₂,a₄).

Означення 3.9. Функція, що утворюється з функцій f ₁, f ₂,..., f _n деякою підстановкою їх одна в одну і перейменуванням аргументів, називається суперпозицією f ₁, f ₂,..., f _n.

Наприклад, у функції f ₁(a₁,a₂,a₃) = a₁+2a₂+7a₃ перейменування a₃ в а₂ приводить до функції f ₁(a₁,a₂,a₂) = a₁+2a₂+7a₂ = f ₂(a₁,a₂) = a₁+9a₂. Перейменування а₁ та а₃ в а₂ приводить до одномісної функції f ₃(a₂) = 10a₂.

Дата добавления: 2014-01-05