Энтропия и количество информации

Получение любой информации - необходимое условие для снятия неопределенности. Задача, которая решается в ходе снятия неопределенности – уменьшение количества рассматриваемых вариантов (уменьшение разнообразия), и выбор одного соответствующего ситуации варианта из числа возможных. Снятие неопределенности дает возможность принимать обоснованные управляющие решения и действовать.

Например, вы зашли в магазин и попросили продать жевательную резинку. Продавец, у которой 16 сортов жевательной резинки, находится в состоянии неопределенности. Но, если вы уточнили: "Orbit", и теперь из 16 первоначальных вариантов продавец рассматривает только 8, вы уменьшили неопределенность в два раза, что соответствует получению 1 бита информации. Если же вы сразу указали пальцем на витрину: "Вот эту!", то неопределенность снимается полностью. Таким жестом вы сообщили продавцу 4 бита информации.

Максимальная неопределенность возникает при наличии нескольких равновероятных альтернатив (вариантов), когда ни один из вариантов не является более предпочтительным. При этом, чем больше равновероятных вариантов рассматривается, тем больше неопределенность и тем больше информации требуется для этого получить.

Минимальная неопределенность будет равна нулю, когда выбор одного варианта сделан - это ситуация полной определенности, означающая, что вся необходимая информация получена.

Величина, характеризующая количество неопределенности в теории информации обозначается символом H и имеет название энтропия, или информационная энтропия.

Энтропия (H) – мера неопределенности, выраженная в битах. Энтропию можно так же рассматривать как меру равномерности распределения (рассеяния) случайной величины.

При полном рассеянии (равномерном распределении) энтропия максимальна, а при полной упорядоченности отсутствует. Примером максимальной величины энтропии (максимального рассеяния) может служить "белый шум" в радиоэфире.

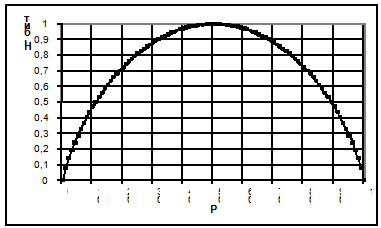
Поведение энтропии для случая двух альтернатив

На рисунке показано поведение энтропии для случая двух вероятных событий, при изменении соотношения их вероятностей

(p, (1-p)).

Максимального значения энтропия достигает тогда, когда обе вероятности равны между собой, т. е. равны ½, а нулевое значение энтропии соответствует случаям (p₀=0, p₁=1) и (p₀=1, p₁=0).

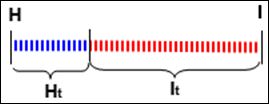
Рис. Связь между энтропией и количеством информации.

Количество информации I и энтропия H характеризуют одну и ту же ситуацию, но с качественно противоположенных сторон.

I – это количество информации, которое требуется для снятия неопределенности H. Можно сказать, что информация есть отрицательная энтропия.

Когда неопределенность снята полностью, количество полученной информации I равно изначально существовавшей неопределенности H.

При частичном снятии неопределенности, полученное количество информации и оставшаяся неснятой неопределенность составляют в сумме исходную неопределенность: H_t + I_t = H.

Из-за этого формулы, по которым рассчитывается энтропия H, являются и формулами для расчета количества информации I, т. е. когда речь идет о полном снятии неопределенности, H в них можно заменить на I.

Дата добавления: 2014-01-05