Переходные процессы при изменении параметров цепи

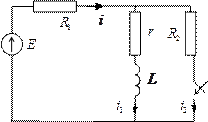Применяя тот же подход, найдем ток через индуктивность 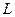. По законам Кирхгофа составим систему из 3 дифференциальных уравнений, из них получим дифференциальное уравнение для требуемой переменной.

.

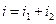Для первого контура второй закон Кирхгофа:

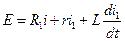
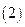
Для второго контура второй закон Кирхгофа:

Выразим из последнего уравнения :

.

Подставим в уравнение 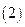уравнение с учетом преобразованного уравнения :

,

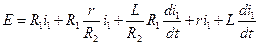получили дифференциальное уравнение относительно :

.

теперь найдем решение полученного уравнения:

.

Чтобы определить 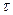, запишем характеристическое уравнение:

.

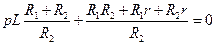
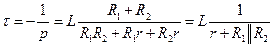До коммутации

,

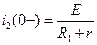тогда по 1 закону коммутации:

.

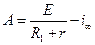Очевидно, характеристика тока через индуктивность будет убывать до какого-то определенного ненулевого значения, поскольку в цепь был включен делитель тока.

Данный метод неудобен, так как слишком громоздок. Рассмотрим более удобные методы для различных цепей.

Если рассматриваемая цепь – первого порядка (содержит один реактивный элемент), то применим следующий метод. Рассмотрим ту же цепь, что и в предыдущем примере. Исключим из нее индуктивность и источник напряжения (с учетом внутреннего сопротивления, он обратится в закоротку).

Дифференциальное уравнение в данном случае будет первого порядка (только один накопитель – индуктивность). Значит конечное выражение для тока имеет вид:

.

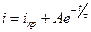В классическом методе расчета основная трудность состояла в определении постоянной времени, постоянная интегрирования сравнительно просто определялась из законов коммутации. Оказывается, 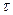можно определить проще:

,

где 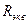- сопротивление цепи относительно зажимов реактивного элементов с учетом внутреннего сопротивления источников ЭДС и тока. В нашем случае:

.

Отметим, что при таком подходе нам не пришлось проделывать трудоемкое решение дифференциальных уравнений. Для емкости выражение для 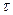приобретает вид:

.

Дата добавления: 2014-01-05