Формула Шеннона. Информации. Кодирование символьных, графических и звуковых данных

Информации. Кодирование символьных, графических и звуковых данных. Структуры данных

Лекция 3. Формулы Шеннона и Хартли. Расчёт количества

В общем случае, энтропия H и количество получаемой в результате снятия неопределенности информации I зависят от исходного количества рассматриваемых вариантов N и вероятностей реализации каждого из них P: {p₀, p₁, …p_N-1}, т. е.

H=F(N, P)

Расчет энтропии в этом случае производится по формуле Шеннона, предложенной им в 1948 году:

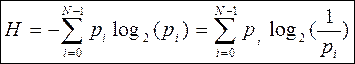
Рассмотрим, что такое логарифм log₂(p), называемый двоичным логарифмом:

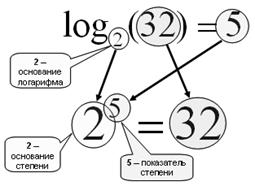
Нахождение логарифма b по основанию a - это нахождение степени, в которую нужно возвести a, чтобы получить b.

log₂(1) = 0 => 2⁰ = 1

log₂(2) = 1 => 2¹ = 2

log₂(8) = 3 => 2³ = 8

log₂(10) = 3,32 => 2^3,32 = 10

Логарифм по основанию 10 называется десятичным:

log₁₀(100) = 2 => 10² = 100

log₁₀(2) = 0,301 => 10^0,301 = 2

Отношение двоичного логарифма к десятичному:

log₂2 / log₁₀2 = 1 / 0,301= 3,32

Основные свойства логарифмов:

log(a^b) = b*log(a)

log(a*b) = log(a) + log(b)

log(a/b) = log(a) - log(b)

log(1/а) = 0 - log(а) = -log(а)

Знак минус в формуле Шеннона не означает, что энтропия – отрицательная величина. Объясняется это тем, что вероятность p_i =< 1 по определению, а логарифм числа меньшего единицы - величина отрицательная.

По свойству логарифма 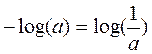, и формулу Шеннона можно записать также во втором варианте - без минуса перед знаком суммы.

интерпретируется как частное количество информации, получаемое в случае реализации i-ого случайного варианта.

Из этого следует сделать вывод, что энтропию по формуле Шеннона можно считать средней характеристикой – математическим ожиданием распределения случайной величины {I₀, I_1,… I_N-1}.

Приведем пример расчета энтропии по формуле Шеннона. Если известно, что мужчин и женщин в учреждении одинаково (два равновероятных варианта), тогда неопределенность, кого вы встретите первым, зайдя в учреждение, составит 1 бит. Проверка этого предположения проведена в таблице 1.

Таблица 1

	pi	1/pi	Ii=log2(1/pi), бит	pi*log2(1/pi), бит
Ж	1/2		log2(2)=1	1/2 * 1=1/2
М	1/2		log2(2)=1	1/2 * 1=1/2
å				H = 1 бит

Если же в учреждении состав работников распределяется так: ¾ - женщины, ¼ - мужчины, тогда неопределенность относительно того, кого вы встретите первым, зайдя в учреждение, будет рассчитана рядом действий, показанных в табл. 2.

Таблица 2

	pi	1/pi	Ii=log2(1/pi), бит	pi*log2(1/pi), бит
Ж	3/4	4/3	log2(4/3) = 0,42	3/4 * 0,42 = 0,31
М	1/4	4/1	log2(4) = 2	1/4 * 2 = 0,5
å				H = 0,81 бит

Как видно, энтропия во втором случае, а, следовательно, и количество информации, получаемой при полной определённости, несколько меньше, чем в первом случае, так как вероятность встретить женщину преобладает, и вам ясно, что скорее вы встретите женщину, чем мужчину.

Дата добавления: 2014-01-05