
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частотные характеристики типовых звеньев
|
|
|
|
Переходя от передаточной функции звена 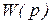 к частотной передаточной функции
к частотной передаточной функции  (по Фурье,
(по Фурье,  ) с помощью операций над комплексными числами, можно найти различные частотные характеристики типовых звеньев.
) с помощью операций над комплексными числами, можно найти различные частотные характеристики типовых звеньев.
В частности, в случае инерционного звена имеем:
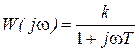 ;
; 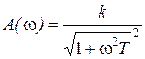 ;
;  ;
;
 ;
;  .
.
Выражения для 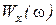 и
и 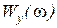 представляют собой уравнение амплитудно-фазовой характеристики в параметрической форме в функции действительного параметра
представляют собой уравнение амплитудно-фазовой характеристики в параметрической форме в функции действительного параметра 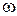 . Изменяя
. Изменяя 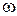 от
от  , построим АФХ. Если из параметрических уравнений исключить
, построим АФХ. Если из параметрических уравнений исключить 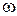 , то получим уравнение АФХ в явном виде. Для этого разделим второе уравнение на первое и найдем
, то получим уравнение АФХ в явном виде. Для этого разделим второе уравнение на первое и найдем 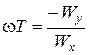 . Подставим это значение
. Подставим это значение  в первое уравнение
в первое уравнение 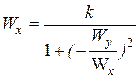 .
.
Приводя к общему знаменателю, преобразуем уравнение к виду

 .
.
Дополним  до полного квадрата, прибавив слева и справа
до полного квадрата, прибавив слева и справа  .
.
Тогда получим 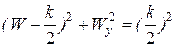 . (2.4.36)
. (2.4.36)
Это уравнение окружности радиуса  с центром в точке
с центром в точке 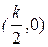 , как показано на рис.2.4.11. При построении АФХ по (2.4.36) не ясно, какой частоте
, как показано на рис.2.4.11. При построении АФХ по (2.4.36) не ясно, какой частоте 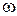 соответствуют точки АФХ. Поэтому следует обратиться к уравнениям в параметрической форме.
соответствуют точки АФХ. Поэтому следует обратиться к уравнениям в параметрической форме.
 Значения
Значения  и
и 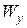 в зависимости от
в зависимости от 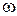 , найденные по параметрическим уравнениям, приведены в табл.2.4.5. Очевидно, что
, найденные по параметрическим уравнениям, приведены в табл.2.4.5. Очевидно, что 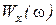 является четной функцией, а
является четной функцией, а 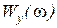 - нечетной, т.е.
- нечетной, т.е. 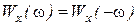 ;
; 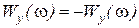 .
.
Следовательно, как и в общем случае, АФХ для 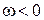 является зеркальным отражением АФХ для
является зеркальным отражением АФХ для  относительно действительной оси. В случае изменения
относительно действительной оси. В случае изменения 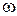 от
от  0 точка пробегает по верхней ветви, характеристики, а в случае изменения
0 точка пробегает по верхней ветви, характеристики, а в случае изменения 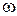 от
от  - по нижней ветви характеристики.
- по нижней ветви характеристики.
Таблица 2.4.5.
Точки АФХ инерционного звена, полученные по параметрическим уравнениям
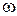
| … | 
| … |  
| |

| 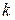
| … | 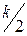
| … | |
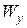
| … | 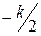
| … |
Логарифмические характеристики инерционного звена рассмотрены в п.2.4.3.
В случае интегрирующего звена имеем
 ;
; 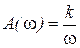 ;
;  ,
, 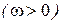 ;
;  ;
; 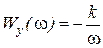 .
.
 Так как
Так как  , то АФХ совпадает с осью ординат (мнимой осью), как показано на рис.2.4.12. В случае изменения
, то АФХ совпадает с осью ординат (мнимой осью), как показано на рис.2.4.12. В случае изменения 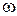 от
от  0 точка пробегает по оси
0 точка пробегает по оси 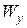 от
от  . В случае изменения
. В случае изменения 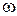 от
от  точка пробегает по оси
точка пробегает по оси 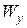 от
от  0.
0.
Для фиксированной частоты  имеем
имеем 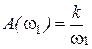 ,
, 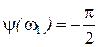 .
.
В случае инерционного звена при непрерывном изменении 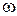 от
от 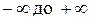 имели плавное изменение АФХ без разрывов, как изображено на рис.2.4.11. В случае интегрирующего звена при переходе
имели плавное изменение АФХ без разрывов, как изображено на рис.2.4.11. В случае интегрирующего звена при переходе 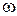 через 0 АФХ разрывается. При
через 0 АФХ разрывается. При 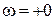 имеем
имеем 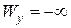 , а при
, а при  имеем
имеем 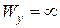 . Возникает неопределенность, где на бесконечности замыкаются ветви АФХ, соответствующие
. Возникает неопределенность, где на бесконечности замыкаются ветви АФХ, соответствующие 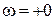 и
и  - слева или справа на рис.2.4.12.
- слева или справа на рис.2.4.12.
Для раскрытия неопределенности рассмотрим звено с передаточной функцией 
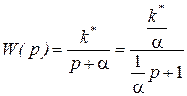 , (2.4.37)
, (2.4.37)
т.е. инерционное звено с коэффициентом усиления 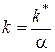 и постоянной времени
и постоянной времени  . АФХ этого инерционного звена изображена на рис 2.4.11. Если
. АФХ этого инерционного звена изображена на рис 2.4.11. Если 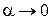 , то инерционное звено (2.4.37) превращается в интегрирующее с передаточной функцией
, то инерционное звено (2.4.37) превращается в интегрирующее с передаточной функцией 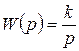 . Очевидно, что в случае
. Очевидно, что в случае 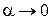 радиус окружности
радиус окружности 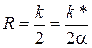 стремится к бесконечности, т.е. АФХ “прижимается” к мнимой оси
стремится к бесконечности, т.е. АФХ “прижимается” к мнимой оси  . При этом замыкание ветвей АФХ для
. При этом замыкание ветвей АФХ для  и
и 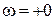 происходит на бесконечности справа (по дуге бесконечно большого радиуса).
происходит на бесконечности справа (по дуге бесконечно большого радиуса).
Таким образом, если нулевой полюс (корень характеристического уравнения) интегрирующего звена сдвинуть влево (из нулевого превратить чуть-чуть в отрицательный), то интегрирующее звено превратится в инерционное, а АФХ при  замкнется на бесконечности справа.
замкнется на бесконечности справа.
Логарифмические характеристики интегрирующего звена

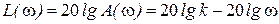 ;
;  .
.
Так как по оси частоты на логарифмических характеристиках откладывается  , то первое уравнение представляет собой прямую линию с наклоном
, то первое уравнение представляет собой прямую линию с наклоном  . Если
. Если 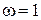 , то
, то 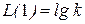 . Если
. Если  , то ЛАХ при
, то ЛАХ при 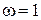 пересекает ось частот. Фазовый сдвиг на всех частотах одинаковый и равен
пересекает ось частот. Фазовый сдвиг на всех частотах одинаковый и равен 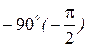 на всех положительных частотах.
на всех положительных частотах.
Логарифмические характеристики колебательного звена рассмотрены в п.2.4.3.
Как было установлено ранее (см.п.2.4.3), для обратных характеристик 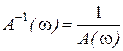 ;
;  . Соответственно
. Соответственно 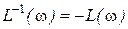 . Следовательно, обратные логарифмические характеристики являются зеркальным отображением прямых относительно оси частот.
. Следовательно, обратные логарифмические характеристики являются зеркальным отображением прямых относительно оси частот.
В частности, в случае дифференцирующего звена с единичным коэффициентом усиления ЛАХ является прямой с наклоном 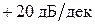 , проходящей через ось частот при
, проходящей через ось частот при 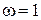 . Передаточные функции и логарифмические характеристики прямых и обратных звеньев с единичным коэффициентом усиления приведены в табл.2.4.6.
. Передаточные функции и логарифмические характеристики прямых и обратных звеньев с единичным коэффициентом усиления приведены в табл.2.4.6.
Логарифмические характеристики звеньев Таблица 2.4.6
| № п/п | Название звена | 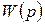
| ЛАХ, ЛФХ |
| Идеальное интегрирующее | 
| 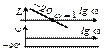
| |
| Инерционное | 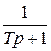
| 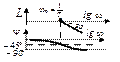
| |
| Колебательное | 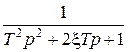
| 
| |
| Идеальное дифференцирующее | 
| 
| |
| Форсирующее | 
| 
| |
| Обратное колебательному | 
| 
|
Из табл.2.4.6 следует:
1. Наклон и соответственно сдвиг по фазе на низких частотах могут дать только интегрирующие или дифференцирующие звенья. Если, например, в передаточной функции имеется r интегрирующих звеньев, то наклон ЛАХ на низких частотах равен  , а сдвиг по фазе соответственно
, а сдвиг по фазе соответственно 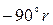 .
.
2. n корням знаменателя (полюсам передаточной функции), т.е. степени знаменателя n, соответствует наклон ЛАХ на верхних частотах, равный  , и в случае минимально фазовой системы - соответственно сдвиг по фазе на высоких частотах, равных
, и в случае минимально фазовой системы - соответственно сдвиг по фазе на высоких частотах, равных  .
.
3. 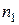 корням числителя (нулям передаточной функции) на высоких частотах аналогично соответствуют наклон ЛАХ, равный
корням числителя (нулям передаточной функции) на высоких частотах аналогично соответствуют наклон ЛАХ, равный  , и сдвиг по фазе
, и сдвиг по фазе 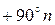 .
.
4. В случае передаточной функции 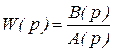 минимально-фазовой системы с n полюсами и n 1 нулями наклон ЛАХ на высоких частотах равен
минимально-фазовой системы с n полюсами и n 1 нулями наклон ЛАХ на высоких частотах равен  , а сдвиг по фазе равен
, а сдвиг по фазе равен 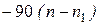 градусов.
градусов.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 686; Нарушение авторских прав?; Мы поможем в написании вашей работы!