
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
И восстановление передаточной функции по ЛАХ
|
|
|
|
Построение логарифмических характеристик систем
Если звенья системы соединены последовательно, то 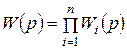 и для модуля и аргумента комплексного коэффициента усиления разомкнутой системы соответственно имеем:
и для модуля и аргумента комплексного коэффициента усиления разомкнутой системы соответственно имеем:
 ;
;  . (2.4.38)
. (2.4.38)
Очевидно, 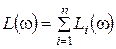 . (2.4.39)
. (2.4.39)
Следовательно, для построения ЛАХ и ЛФХ нужно просуммировать соответствующие характеристики отдельных звеньев.
Пример 2.4.3. Построить ЛАХ и ЛФХ по передаточной функции
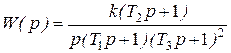 ,
,
где  ;
; 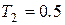 с;
с; 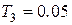 с. Соответственно сопрягающие частоты равны
с. Соответственно сопрягающие частоты равны 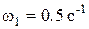 ;
; 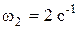 ;
;
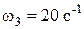 .
.
Передаточную функцию представим в виде произведения передаточных функций интегрирующего звена 
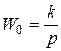 ; инерционных звеньев
; инерционных звеньев 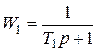
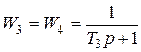 и форсирующего
и форсирующего  . Логарифмические амплитудные и фазовые характеристики отдельных звеньев, а также результирующие ЛАХ и ЛФХ системы построены на рис.2.4.13 и 2.4.14.
. Логарифмические амплитудные и фазовые характеристики отдельных звеньев, а также результирующие ЛАХ и ЛФХ системы построены на рис.2.4.13 и 2.4.14.

| |||
|
На рис.2.4.13 жирными линиями показаны асимптотические ЛАХ звеньев. Характеристики двух инерционных звеньев с передаточными функциями 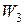 и
и 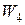 на графиках сливаются, но их необходимо учитывать дважды. Это касается также и ЛФХ этих звеньев. Для построения результирующей ЛАХ к ЛАХ интегрирующего звена последовательно добавлялись характеристики остальных звеньев при перемещении вдоль оси частот слева направо по мере встречи сопрягающих частот. После очередной частоты сопряжения наклон ЛАХ изменялся на
на графиках сливаются, но их необходимо учитывать дважды. Это касается также и ЛФХ этих звеньев. Для построения результирующей ЛАХ к ЛАХ интегрирующего звена последовательно добавлялись характеристики остальных звеньев при перемещении вдоль оси частот слева направо по мере встречи сопрягающих частот. После очередной частоты сопряжения наклон ЛАХ изменялся на 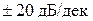 . Приращение наклона соответствовало звену, которому принадлежала сопрягающая частота.
. Приращение наклона соответствовало звену, которому принадлежала сопрягающая частота.
Анализируя результаты примера и характеристики типовых звеньев (табл.2.4.6), можно сделать вывод, что ЛАХ разомкнутой системы можно построить сразу, минуя промежуточные построения ЛАХ звеньев и суммирование их, по правилу:
1. Найти сопрягающие частоты и отложить их на оси частот. Ось ординат провести для удобства левее самой низкой сопрягающей частоты.
2. При ω = 1 отложить 20 lgk и через эту точку провести прямую с наклоном -20 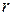 дБ/дек, если в системе имеется
дБ/дек, если в системе имеется 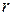 интегрирующих звеньев, или с наклоном +20
интегрирующих звеньев, или с наклоном +20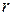 дБ/дек, если в системе имеется
дБ/дек, если в системе имеется 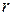 дифференцирующих звеньев (при
дифференцирующих звеньев (при 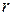 = 0 низкочастотная асимптота ЛАХ параллельна оси абсцисс).
= 0 низкочастотная асимптота ЛАХ параллельна оси абсцисс).
3. При прохождении слева направо каждой из частот сопряжения характеристика испытывает приращение наклона -20 дБ/дек (для инерционного звена), -40 дБ/дек (для колебательного звена), +20 дБ/дек (для форсирующего звена), +40 дБ/дек (для звена, обратного колебательному). Если сопрягающие частоты нескольких звеньев одинаковы, то приращение наклона ЛАХ равно суммарному приращению от всех звеньев. Если имеется хотя бы одна частота сопряжения, меньшая единицы, то точка 20 lgk при ω = 1 не будет лежать на результирующей ЛАХ.
4. Ввести поправку к асимптотической ЛАХ при наличии колебательных или обратных им звеньев.
Для контроля правильности построения ЛАХ и ЛФХ полезно помнить, что наклон ЛАХ в области высоких частот (ω → ∞) равен 20 (m-n) дБ/дек, где m - порядок числителя, n - порядок знаменателя передаточной функции системы. Кроме того, 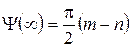 ;
; 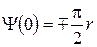 , (2.4.40)
, (2.4.40)
где знак минус берётся при наличии 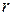 интегрирующих, а плюс -
интегрирующих, а плюс - 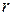 дифференцирующих звеньев. Из анализа методики построения ЛАХ по передаточной функции вытекает возможность обратного перехода, т. е. восстановления передаточной функции минимально-фазовой системы по ЛАХ.
дифференцирующих звеньев. Из анализа методики построения ЛАХ по передаточной функции вытекает возможность обратного перехода, т. е. восстановления передаточной функции минимально-фазовой системы по ЛАХ.
При восстановлении передаточной функции минимально-фазовой системы по ЛАХ записываем дробь, в числителе которой ставим общий коэффициент усиления 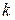 и далее делаем начинку дроби. По величине наклона низкочастотного участка определяем количество интегрирующих или дифференцирующих звеньев (формально отрицательному наклону соответствуют интегрирующие звенья и, соответственно, множитель
и далее делаем начинку дроби. По величине наклона низкочастотного участка определяем количество интегрирующих или дифференцирующих звеньев (формально отрицательному наклону соответствуют интегрирующие звенья и, соответственно, множитель  в знаменателе, положительному наклону – множитель
в знаменателе, положительному наклону – множитель  в числителе,
в числителе, 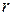 - кратность наклона 20-ти децибелам). В случае нулевого наклона интегрирующие или дифференцирующие звенья отсутствуют. Далее при движении слева направо по мере встречи частот сопряжения анализируем приращение (изменение) наклона. Если приращение составляет +20 Дб/дек, то в числитель записываем
- кратность наклона 20-ти децибелам). В случае нулевого наклона интегрирующие или дифференцирующие звенья отсутствуют. Далее при движении слева направо по мере встречи частот сопряжения анализируем приращение (изменение) наклона. Если приращение составляет +20 Дб/дек, то в числитель записываем  для форсирующего звена вида
для форсирующего звена вида  , если приращение составляет -20 Дб/дек, то в знаменатель записываем
, если приращение составляет -20 Дб/дек, то в знаменатель записываем  для инерционного звена вида
для инерционного звена вида 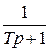 . В случае приращения наклона +40 Дб/дек в числитель записываем два форсирующих звена
. В случае приращения наклона +40 Дб/дек в числитель записываем два форсирующих звена 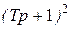 , в случае приращения наклона -20 Дб/дек в знаменатель записываем
, в случае приращения наклона -20 Дб/дек в знаменатель записываем 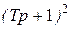 для двух инерционных звена вида
для двух инерционных звена вида 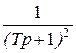 . Если на ЛАХ показана поправка на коэффициент затухания
. Если на ЛАХ показана поправка на коэффициент затухания 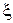 , то вместо двух форсирующих или инерционных звеньев записываем обратное колебательному или колебательное звено (множитель
, то вместо двух форсирующих или инерционных звеньев записываем обратное колебательному или колебательное звено (множитель  в числителе или в знаменателе). Если кратность наклона 3 и более, то записываем соответствующее количество звеньев с одинаковыми частотами сопряжения. Для определения коэффициента усиления находим точку пересечения продолжения низкочастотного участок ЛАХ с вертикальной прямой с абсциссой
в числителе или в знаменателе). Если кратность наклона 3 и более, то записываем соответствующее количество звеньев с одинаковыми частотами сопряжения. Для определения коэффициента усиления находим точку пересечения продолжения низкочастотного участок ЛАХ с вертикальной прямой с абсциссой 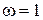 и по ординате этой точки
и по ординате этой точки 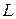 определяем
определяем  .
.
В случае минимально-фазовой системы в двучленах и трехчленах, упомянутых выше, берем знаки “+”. Если бы имелись не минимально-фазовые звенья, то нужно было бы взять знак “-“. При этом ЛАХ осталась бы прежней, а ЛФХ была бы другой. Поэтому в случае минимально-фазовой системы восстановление однозначно и нет необходимости контролировать АФХ.
Пример 2.4.4. Восстановить передаточную функцию минимально-фазовой системы по ЛАХ рис.2.4.15.
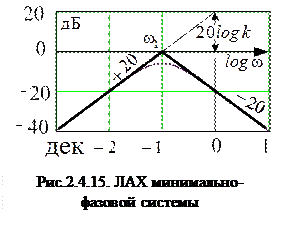 В соответствие с приведенными соображениями передаточная функция минимально-фазовой системы будет равна
В соответствие с приведенными соображениями передаточная функция минимально-фазовой системы будет равна
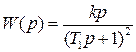 .
.
Из рис.2.4.15 имеем 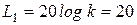 дБ и
дБ и 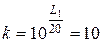 с,
с,  . Обратим внимание, что
. Обратим внимание, что 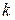 > 1, ЛАХ на всех частотах расположена ниже оси частот.
> 1, ЛАХ на всех частотах расположена ниже оси частот.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 3913; Нарушение авторских прав?; Мы поможем в написании вашей работы!