Урни та кульки. 1.1.2.1 Урнова схема: вибір без повернення, з урахуванням порядку

1.1.2.1 Урнова схема: вибір без повернення, з урахуванням порядку

1.1.2.2 Урнова схема: вибір без повернення та без урахування порядку

1.1.2.3 Урнова схема: вибір з поверненням та з урахуванням порядку

1.1.2.4 Урнова схема: вибір з поверненням та без урахування порядку

1.1 Основні формули комбінаторики

У даному розділі ми займемося підрахунком кількості шансів.

Кількість шансів – це число можливих результатів будь-якої дії (монетка, кубик, карти, тощо) або число способів зробити цю дію.

1.1.1 Теорема про перемноження шансів

Теорема 1. Нехай є , груп елементів, причому 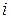-та група містить елементів, 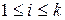. Виберемо з кожної групи по одному елементу. Тоді загальна кількість способів, якими можна зробити такий вибір, дорівнює

. (1.1)

Зауваження 1. Представимо результат вибору, описаного у теор.1 у вигляді набору , в якому – вибраний з 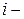ої групи елемент. Тоді загальна кількість різних наборів також дорівнює .

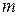Доведення. З елементом ми можемо утворити пар: , , 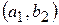…, . Стільки ж пар можна скласти з елементом , стільки ж – з елементом 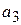і з будь-яким іншим з 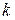елементів множини . Тобто всього можливо пар, у яких перший елемент вибрано з множини , а другий – з множини .

Приклад 1. В одного студента 5 книг, у іншого – 9. Усі книги різні. Скількома способами студенти можуть провести обмін:

а) 1 книгу на 1 книгу?

Дата добавления: 2014-01-05