Урни та кульки

Маємо урну, що містить 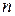занумерованих кульок. Ми вибираємо 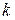кульок. Скількома способами можна вибрати 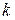кульок з ?

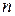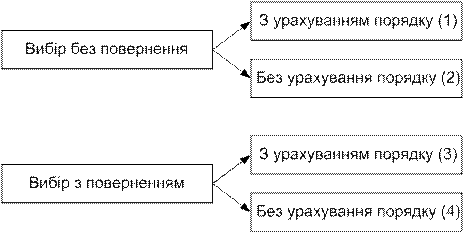
Рис. 1.1 – Чотири схеми відбору

1.1.2.1 Урнова схема: вибір без повернення з урахуванням порядку

Теорема 2. Загальна кількість вибірок у схемі вибору елементів з 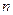без повернення та з урахуванням порядку визначається за формулою

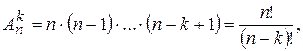(1.2)

де 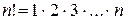, та називається кількістю розміщень з 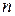елементів по 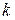елементів.

Доведення: 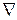1-й ;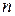

2-ий ;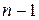

3-ий ;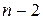

…;

k-ий .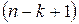

За теор.1 загальна кількість способів вибору дорівнює

.

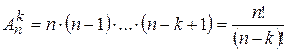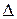
Приклад 2. 10 спортсменів розіграють одну золоту, одну срібну та одну бронзову медалі. Скількома способами ці медалі можуть бути розподілені між спортсменами.

Приклад 3. Скільки словників потрібно видати, щоб можливо було безпосередньо виконати переклади з будь-якої з п’яти мов: російської, англійської, французької, німецької, італійської – на будь-яку з цих п’яти мов?

Висновок 1. Кількість можливих перестановок множини з 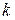елементів є .

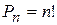Доведення: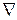Перестановка є ні що інше, як .

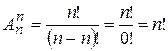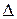
Приклад 4. У пасажирському потязі 9 вагонів. Скількома способами можливо розсадити в потязі 9 людей за умови, що всі вони повинні їхати в різних вагонах?

1.1.2.2 Урнова схема: вибір без повернення та без урахування порядку

Теорема 3. Загальна кількість вибірок у схемі вибору елементів з 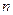без повернення та без урахування порядку визначається формулою

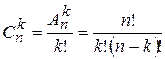, (1.3)

і називається кількістю поєднань з 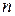елементів по 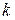елементів.

Доведення. 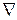Згідно із висновком 1 переставляючи елементи можна отримати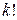комбінацій, тобто, комбінацій без урахування перестановок повинно бути у 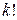разів менше, ніж з їх урахуванням, тобто

.

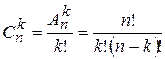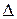
Приклад 5. В одного студента 5 книг, у іншого – 9. Усі книги різні. Скількома способами студенти можуть провести обмін 3книги на 3 книги?

1.1.2.3 Урнова схема: вибір з поверненням та з урахуванням порядку

Теорема 4. Загальна кількість вибірок у схемі вибору 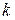елементів з 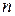з поверненням та з урахуванням порядку визначається формулою

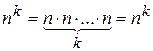, (1.4)

Доведення.

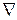1-й 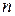спосіб;

2-й 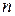спосіб;

…;

k - 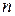спосіб. За теор.1: .

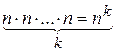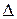
Приклад 6. Скільки тризначних чисел можливо створити з цифр 1, 2, 3, 4, 5, 6, 7 якщо кожна цифра може входити у число більше одного разу?

1.1.2.4 Урнова схема: вибір з поверненням та без урахування порядку

Теорема 5. Загальна кількість вибірок у схемі вибору елементів з 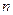з поверненням та без урахуванням порядку визначається за формулою

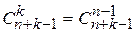, (1.5)

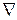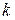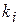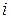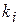Доведення. Розглянемо докладно, чим відрізняються один від одного два різних результати такої схеми вибору. Нам не важливий порядок номерів, тобто ми враховуємо тільки, скільки разів у нашому наборі з номерів кульок з'явився кожен номер. Тому результат вибору можна представити набором чисел , у якому – число появ кулі з номером у наборі, і . Числа приймають значення з множини 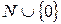. Два результати вибору в схемі вибору з поверненням без урахування порядку розрізняються, якщо відповідні їм набори не співпадають (тут порядок проходження елементів 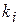враховується).

Уявімо собі інший експеримент, що має точно такі ж результати, і порахуємо їх кількість. Є 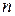ящиків, в яких розміщуються 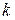кульок. Нас цікавить тільки число куль у кожному ящику. Результатом експерименту знову є набір чисел , де 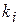дорівнює кількості куль у ящику з номером 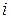та . Числа 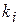приймають натуральні значення або дорівнюють нулю.

А тепер зобразимо результат такого розміщення у вигляді схеми, в якій вертикальні лінії позначають перегородки між ящиками, а точки – кул, що знаходяться в ящиках кульки:

Перекладемо одну кулю з першого ящика в другій і зобразимо таким же чином ще два результати розміщення:

Бачимо, що всі розміщення можна отримати, змінюючи між собою кульки і перегородки, або розставляючи 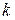куль на 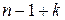місцях. Число 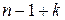отримується так: у 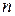ящиків є рівно 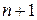перегородок, враховуючи крайні, але з них переміщати можна лише 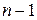внутрішню перегородку. Таким чином, є 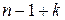місць, які можна зайняти кулями або внутрішніми перегородками. Перебравши всі можливі способи розставити 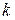куль на цих 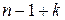місцях (заповнюючи решту місць перегородками), переберемо всі потрібні розміщення.

Залишилося відмітити, що існує 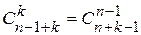способів розставити 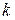куль на 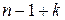місцях. Саме стільки є способів вибрати з 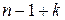номерів місць 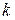номерів місць для куль.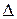

Вправа.

1. Знайти кількість способів розкласти натуральне число 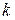в суму 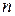цілих невід'ємних доданків, якщо важливий порядок проходження цих доданків.

2. Знайти число різних похідних порядку 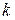функції 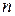змінних.

3. (Д/з) Знайти число можливих результатів підкидання двох гральних кісток, якщо кістки вважаються нерозрізненими. Те ж саме для трьох гральних кісток.

Література

1. Чернова Н. И. Теория вероятностей. Лекции. 1 курс ЭФ, отделение «математические методы и исследование операций в экономике». Новоибирск, 2002.

2. Чистяков В. П. Курс теории вероятностей: Учеб. - 3-е изд., испр. - М.: Наука, Гл. Ред. Физ.-мат. Лит. - 1987.

3. Андрухаев Х. М. Сборник задач по теории вероятностей. М.: «Просвещение», 1985 г.

4. Сидоренко В.М.Методичні вказівки до практичних занять та самостійної роботи з дисципліни “Теорія ймовірностей та математична статистика” для студентів спеціальності 7.091501 “Комп’ютерні системи та мережі” для всіх форм та термінів навчання.

Дата добавления: 2014-01-05