Диффузия в пленочных структурах

При производстве ЭС широко используются различные многослойные тонкопленочные структуры, в которых диффузионные процессы решающим образом влияют на качество изделия и стабильность его во времени. Изучение диффузионных процессов в тонких пленках
представляет значительный интерес и
для понимания диффузионных явлений.
В неотожженных тонких пленках
диффузия может протекать быстрее,
чем в массивных материалах, из-за
высоких концентраций вакансий и гра-
ниц зерен, обусловленных мелкокрис-
талличностью осаждаемых пленок.

Как указывалось, вид диффузион-ного процесса зависит от природы
участвующих в нем веществ и характе-
ра их межатомного взаимодействия, определяемого диаграммой состояния.
Рассмотрим диффузионный процесс в простейшей системе, состоящей из па-
ры металлов М₁ — М₂ (Au — Ag), кото-
рые растворяются друг в друге в лю-
бых пропорциях. В такой системе при плоской поверхности разде-
ла зависимость концентрации от расстояния на границе раздела
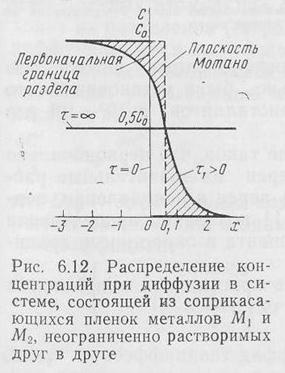
претерпевает разрыв при х =0 (рис. Д.12). По прошествии некоторого времени 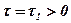распределение концентрации становится не-
прерывным. Если соприкасающиеся пленки имеют одинаковую тол
щину, то при 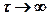концентрации станут равными 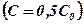, а их распределение изобразится прямой линией, параллельной оси
абсцисс.

Металлы М₁ и М₂ имеют коэффициенты диффузии D₁ и D₂.
В общем случае 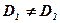и зависимость концентрации от расстояния
при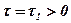будет иметь вид, изображенный на рис. Д.12. В одну
сторону от первоначальной границы раздела продиффундировало
больше вещества, чем в другую. Таким образом, граница раздела,
для которой 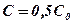, перемещается из точки 0 в точку 0₁. По мере
протекания диффузии граница раздела становится все менее чет-
кой, а выбор начала отсчета координаты х — менее очевидным. Новую границу (плоскость) раздела называют плоскостью Мотано.
Ее определяют как плоскость, полный диффузионный поток через
которую равен нулю (т. е. диффузионные потоки, протекающие через эту плоскость в противоположных направлениях, равны). Положение плоскости Мотано на рис. 6.12 можно найти, приравнивая
площади заштрихованных областей.

Физико-химические основы ионно-плазменных процессов получения пленок

Характеристика плазмы и ее параметры

Ионно-плазменные методы получения пленок универсальны это подтверждается многообразием различных ТП, осуществляемых с ее помощью: очистка подложек, напыление слоев, травление с целью созда­ния заданного рисунка ИМС, отжиг пленок, окисление. Одно из их основных преимуществ невысокие температуры процессов, отсутствие жидких химических реагентов и растворителей.

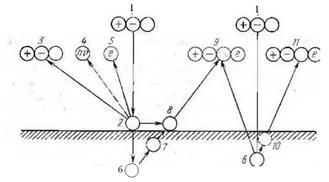
В плазме атомные частицы (нейтральные атомов, по­ложительные и отрицательные ионы) взаимодействуют с поверхностью твердого те­ла по сложным механизмам. Бомбардирующие первичные атомные частицы вызы­вают эмиссию вторичных ионов, электронов, нейтральных атомов (катодное распыление), радикалов и химически активных частиц в зависимости от энергии и природы первичных частиц и от свойств и природы самой поверхности. Схема про­цессов, происходящих при взаимодействии атомных частиц с по­верхностью твердого тела, показана на рис. П.1.

Рис. П1. Схема процессов, происходящих при взаимодей­ствии атомных частиц с поверхностью твердого тела: 1 — поток атомных частиц; 2 — атомная частица, взаимодействую­щая с поверхностью; 3— упругое рассеяние положительного, отри­цательного ионов и нейтрального атома; 4 — испускание электро­магнитного излучения в момент соударения; 5 — электроны, выбиваемые из бомбардирующих частиц в момент соударения с по­верхностью; 6 —частица, внедренная внутрь мишени; 7 — введренная частица, диффундирующая к поверхности. 8 — адсорбиро­ванные частицы, диффундирующие вдоль поверхности: 9— части­цы, покинувшие поверхность за счет теплового испарения; 10 — частицы, выбиваемые из мишени к поверхности; 11 — частицы, вы­битые из мишени и пленок и покинувшие поверхность  

Плазмой называют ионизированный газ, который состоит из трех видов частиц: ионов, электронов и нейтральных атомов (мо­лекул). Электрические силы, связывая разноименно заряженные частниы, обеспечивают квазииейтральиость плазмы.

Произведем оценку напряженности полей, возникающих при наруше­нии нейтральности плазмы, предположим, что в некотором объеме произошло полное разделение зарядов и внутри его остались заряды только одного знака. При разделении зарядов в плазме возни­кает электрическое поле, описываемое уравнением Пуассона:

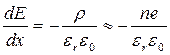(393)

где Е — напряженность электрического поля, В/м; х — координа­та, м; ρ— плотность электрического заряда, Кл/см³; ε_r—относи­тельная диэлектрическая проницаемость среды (для газов ε_r =1); ε_о=8,85-Ф/м — электрическая постоянная; п — концентрация заряженных частиц в плазме, м^-3; е=1,6-10^-19 Кл — заряд элек­трона.

Интегрируя выражение (393) от 0 до X, получим

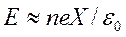(394) 408)

где X — линейный размер области нарушения нейтральности плаз­мы, м.

Потенциал плазмы в области разделения зарядов

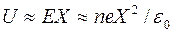(395) (409)

Допустим, что полностью ионизированная плазма получена из водорода, находящегося первоначально при нормальной температу­ре 293 К и давлении 133 Па. В каждом кубическом миллиметре такой плазмы число ионов (электронов) равно первоначальному числу атомов водорода, т. е. 7·10¹³. В этом случае Е=10¹³ В/м. Если, например, резкое нарушение квазинейтральности происходит в элементе объемом около 1 мм³, то Е=10¹² В/м, U=10⁹ В. Такое разделение зарядов нереально. Даже в более разреженной плазме резкое нарушение квазинейтральности в указанном объеме немед­ленно скомпенсируется возникающими полями. Поле будет вытал­кивать из объема, где произошла декомпенсация зарядов, частицы одного и втягивать в эту область частицы другого знака.

Тем не менее, при заданных концентрации и температуре в плаз­ме всегда можно выделить некоторый малый объем с линейным размером δ_D, который удовлетворяет следующему условию: при х<<δ_D в пределах объема с линейным размером х разделение заря­дов происходит без существенного влияния на движение частиц; при х>>δ_D концентрации частиц противоположных знаков в указан­ном объеме почти одинаковы. Область, ограниченная линейным размером δ_D, характеризуется тем, что в ней потенциальная энергия заряженной частицы (при полном разделении зарядов) и энергия теплового движения частиц (kT) имеют одинаковый порядок.

Впервые размер δ_D был введен П. Дебаем при разработке тео­рии сильных электролитов. Затем его использовали в физике плаз­мы, назвав дебаевским радиусом (дебаевской длиной).

Для измерения температуры плазмы воспользуемся энергетиче­ской системой единиц, в которой постоянная Больцмана k = 1, а температура плазмы Θ измеряется в электрон-вольтах (1 эВ = = 1,6- 10^-19 Дж). При этом

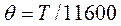, (396) (410)

где Т — температура плазмы, К.

При заданном обозначении температура соответствует величине, характеризующей тепловую энергию частиц.

Ионизированный газ называют плазмой в том случае, когда де-6 пеке кий радиус мал по сравнению с объемом, занимаемым этим газом [1]. Численное значение 6д можно получить, используя (395) и подставляя δ_D вместо X в выражение для потенциальной энергии:

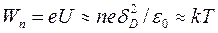(397) (411)

Отсюда 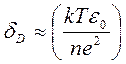(398) (412)

При подстановке значений констант получим

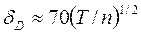(399) (413)

Так как дебаевский радиус характеризует пространственный масштаб областей декомпенсации зарядов, то время τ, в течение ко­торого эти области существуют, можно определить, разделив раз­мер δ_D на скорости υ_e наиболее быстрых частиц — электронов:

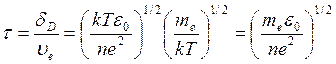(400) (414)

где m_е — эффективная масса электрона, кг.

Величина 1/τ является частотой собственных электростатических колебаний, возникающих в плазме при смещении групп электронов из равновесного состояния. Ее называют плазменной или ленгмю-ровской частотой. Плазменная частота

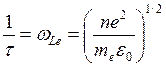(401) (415)

Обычно плазму получают с помощью внешних источников элект­рического питания за счет создания различных форм разряда в га­зах. При этом энергия передается электронам, которые определяют в основном электрический ток плазмы. При столкновении с ионами электроны передают им энергию, которая не превосходит 4 m_e/mi. Поскольку масса электрона значительно меньше массы иона, элект­рон должен испытать тысячи соударений для полной передачи из­лишка своей энергии ионам. Поэтому практически во всех ТП с использованием плазмы электронная температура превосходит ион­ную.

Под действием электрического поля или градиента давления в плазме возникают направленные потоки частиц: в первом случае возникает электрический ток, во втором — диффундируют частицы. Ток через плазму обеспечивается главным образом движением электронов. Движущиеся под действием силы поля еЕ электроны испытывают торможение при столкновении с ионами. Каждое столкновение приводит к потере импульса m_eυ_e. При частоте столк­новений v _ei(с^-1) сила торможения равна m_eυ_e v _ei. Условие равнове­сия между силой, с которой действует на электроны электрическое поле, и силой торможения можно записать в виде

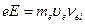(401) (416)

Плотность тока в плазме

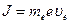(402) (417)

В соответствии с (416) и (417)

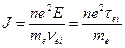(403) (418)

где τ_ei — среднее время между двумя столкновениями частиц.

Уравнение (403) выражает закон Ома для плазмы. При этом удельная проводимость плазмы

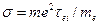(404) (419)

Время τ_еi можно определить, зная длину свободного пробега ча­стиц λ _ei при электронно-ионном взаимодействии в плазме. Длина свободного пробега частиц

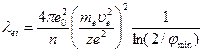(405) (420)

где z e — заряд рассеивающего центра (иона); j_min — минимальный угол рассеяния частицы.

Предполагая, что распределение электронов по энергиям под­чиняется закону Максвелла — Больцмана, перейдем от скорости υ_e к электронной температуре, используя следующее выражение

для средней квадратичной скорости: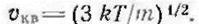

Подставив численные значения констант в (405), получим уравнение для определения средней длины свободного пробега (для водородной плазмы):

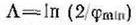
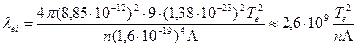(406) (421)

где — кулоновский логарифм.

Кроме длины свободного пробега λ _{е i} можно ввести ряд других параметров для характеристики процессов столкновения электро­нов с ионами. Эффективная площадь сечения таких столкновений

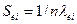(407) (422)

Средине время между двумя соударениями и их частота могут быть найдены из формул

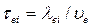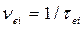; . (408)

При больших изменениях n и Т _е [см. (406)] Λ= 10—20. По­скольку при использовании плазмы в технологических целях достаточно грубых оценок величин, характеризующих процессы столкновения частиц, примем Λ = 15. В этом случае параметры S _ei, τ_еi,, ν_ei можно вычислить по следующим формулам;

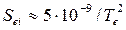
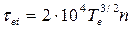
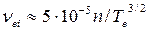(409)

Подставляя значение τ _ei в уравнение (404), получим среднюю удельную проводимость (Ом-м)^-1:

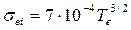(410)

Удельная проводимость плазмы быстро возрастает с температу­рой и уже при 10⁷К становится равной удельной проводимости ме­ди при комнатной температуре.

Таким образом, плазма является энергетически активной сре­дой, обладающей определенными электро- и теплопроводностью. Ее используют в ряде физических и химических процессов, приме­няемых в технологии РЭА, например для испарения (распыления), травления, химического разложения (активации) и др.

Поскольку в плазме легко осуществить целенаправленную диф­фузию частиц под действием градиента того или иного фактора, ее применяют и для массопереноса вещества из одной точки про­странства в другую. Исследование влияния электро-, тепло- и мас­сопереноса на процессы формирования плазмы и с ее помощью рабочих элементов РЭА являются важными для многих ТП произ­водства РЭА.

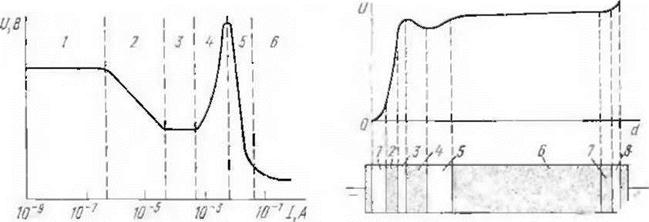
Низкотемпературная плазма формируется с помощью газового разряда в пространстве между двумя элек­тродами. Электроды выполняются в виде плоских или изогнутых поверхностей, к которым подводится высокое напряжение (десятки киловольт). Тип разряда зависит от давления газа, приложенного напряжения и концентрации электронов, которые влияют на длину разрядного промежутка и плотность разрядного тока. Давление газа в разрядном пространстве поддерживается в пределах 0,13— 20 Па. Температура такой плазмы обычно не превышает 10⁴—10⁵ К, концентрация заряженных частиц составляет 10¹⁴—10²¹ м^-3. На рис. П.2 приведена вольт-ампериая характеристика (ВАХ) газово­го разряда между двумя плоскими электродами.

При достижении определенного напряжения (пробивного) на­ступает пробой газового промежутка. В области 1, известной под названием области таунсендовского разряда, при постоянном на­пряжении между электродами ток увеличивается. При дальнейшем увеличении тока (область 2) достигается область нормального тлеющего разряда (область 3). Если сила тока превышает опреде­ленное значение, то по мере дальнейшего увеличения тока напря­жение между электродами растет — наступает аномальный тлею­щий разряд (область 4). При дальнейшем увеличении тока напря­жение между электродами быстро падает (область 5) и возникает дуговой разряд (область 6), Характерной чертой дугового разряда является то, что он может возникать как при высоком, так и при низком давлении. На рис. П.3 изображена схема и распределение потенциала между электродами при тлеющем разряде при давле­нии 1,33—1,3- 10^-2 Па.

Носителями заряда в межэлектродном промежутке служат электроны и ионы, движущиеся вдоль силовых линий электрическо­го поля. В тлеющем разряде давление газа р так велико, что сред­ние длины свободного пробега ионов λ _i и распыленных атомов ми­шени λ _а малы по сравнению с расстоянием d между электродами. Поэтому возможны многократные столкновения между газовыми частицами и электронами, что приводит к образованию ионов, бом­бардирующих поверхность катода (мишени). Эти ионы выбивают (распыляют) атомы из материала катода (мишени). Последние, однако, частично могут ионизироваться и диффундировать обратно к катоду, что снижает эффективность процесса распыления. При существовании разряда соблюдается равенство pd= const (закон Пашена).

Рис. 10.3. Схема распределения потенциала м ежду эл ект рода м и: 1— темное астоновое пространство-, 2 — первое ка­тодное свечение; 3 — темное катодное пространст­во; 4 — отрицательное тлеющее свечение; 5 — фа­радеево темное пространство; 6—положительный столб разряда; 7—анодное свечение; 8 —темное-анодное простраистно  

Рис. 10.2. ВАХ газового разряда

Для увеличения длины свободного пробега используют газовый разряд при низких давлениях, что позволяет достигнуть значений λ _i и λ _a, соизмеримых с расстоянием между электродами. Однако в этих условиях из-за увеличения длины свободного пробега элект­ронов λ _e снижается степень ионизации газа. Чтобы избежать это­го, применяют магнитное поле или облучение межэлектродного про­странства электронным лучом, для чего в систему вводят источник электронов — электронную пушку.

Характер физико-химических процессов, протекающих в плазме, определяется энергией ионов, составом плазмы и механизмом вза­имодействия частиц плазмы между собой и с поверхностью обра­батываемого материала. Реальная плазма существует в широкой области температур и давлений; различные ее виды отличаются по плотности и энергии частиц.

Состав плазмы сложный; он определяется ионно-молекулярны­ми взаимодействиями типа (411)

При взаимодействии потока ионов с поверхностью твердого те­ла протекают сложные физико-химические процессы, различные для различных энергий ионов. В общем случае удельная энергия ионов W _i пропорциональна уско­ряющему напряжению U _i и плот­ности тока j _i.

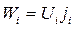(412)

Если обозначить W ₁ - удельную энергию пучков ионов, достаточ­ную для возникновения электронно-ионной эмиссии; W₂ — удельную энергию, необходимую для стимулирования химических реак­ций, протекающих на бомбарди­руемой поверхности; W₃ — удельную энергию, требуемую для очистки и травления поверхности; W₄ — удельную энергию, идущую на катодное распыление и трав­ление слоев; W ₅ — удельную энергию, достаточную для локального нагрева бомбардируемой поверхности с целью ее испарения или фигурной обработки твердого тела и пленки; W ₆ — удельную энер­гию пучка ионов, необходимую для внедрения их внутрь твердого тела (ионной имплантации). Соотношение между этими величина­ми можно записать в виде следующего неравенства:

(413)

Из неравенства (413) следует, что существуют экстремальные значения энергии бомбардирующих ионов, в диапазоне которых бу­дет идти распыление. При значениях энергии, меньших пороговой, распыления не наблюдается. При значениях энергии, больших энергии имплантации ионов, распыление отсутствует из-за относительно глубокого внедрения бомбардирующего иона в мишень. Вся энер­гия в последнем случае расходуется на радиационные поврежде­ния решетки мишени.

[1]Это определение принадлежит И. Ленгмюру, который в 1923 г. ввел тер­мин «плазма».

Дата добавления: 2014-01-05