Деревья

Дерево – это совокупность элементов, называемых узлами (один из которых определен как корень), и отношений («родительских»), образующих иерархическую структуру узлов. Вообще говоря, древовидная структура задает для элементов дерева (узлов) отношение «ветвления», которое во многом напоминает строение обычного дерева.

Формально дерево (tree) определяется как конечное множество T одного или более узлов со следующими свойствами: а)Существует один выделенный узел, а именно – корень (root) данного дерева; А б)Остальные узлы (за исключением корня) распределены среди m>=0 непересекающихся множеств T 1, T 2, …, T m, и каждое из этих множеств, в свою очередь, является деревом; деревья T 1, T 2,..., T m называются поддеревьями данного корня.

Это определение является рекурсивным: дерево определено на основе понятия дерево. Рекурсивный характер деревьев можно наблюдать и в природе, например, почки молодых деревьев растут и со временем превращаются в ветви (поддеревья), на которых снова появляются почки, которые также растут и со временем превращаются в ветви (поддеревья) и т.д. Можно привести еще одно формальное определение дерева: Один узел является деревом. Этот же узел также является корнем этого дерева. Пусть n – это узел, а T 1, T 2,... T m – деревья с корнями n 1, n 2, … n m соответственно. Можно построить новое дерево, сделав n родителем узлов n 1, n 2, … n m. В этом дереве n будет корнем, а T 1, T 2,... T m – поддеревьями этого корня. Узлы n 1, n 2, …,n m называются сыновьями узла n.

Из приведенных выше определений следует, что каждый узел дерева является корнем некоторого поддерева данного дерева. Количество поддеревьев узла называется степенью(degree) этого узла. Узел с нулевой степенью называется концевым узлом(terminal node) или листом(leaf). Неконцевой узел называется узлом ветвления(branch node). Каждый узел имеет уровень(level), который определяется следующим образом: уровень корня дерева равен нулю, а уровень любого другого узла на единицу выше, чем уровень корня ближайшего поддерева, содержащего данный узел. Рассмотрим эти понятия на примере дерева с семью узлами (см. рисунок). Узлы часто изображаются буквами, они так же, как и элементы списков могут быть элементами любого типа.

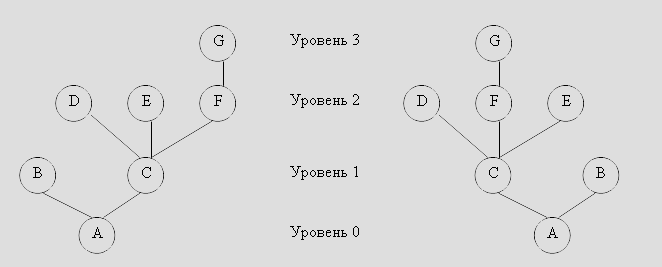
Узел A является корнем, который имеет два поддерева { B } и { C, D, E, F, G }. Корнем дерева{ C, D, E, F, G } является узел C. Уровень узла C равен 1 по отношению ко всему дереву. Он имеет три поддерева { D }, { E }и { F, G }, поэтому степень узла C равна 3. Концевыми узлами (листьями) являются узлы B, D, E, G.

Если в п.б) данного выше определения имеет значение относительнгый порядок поддеревьев T 1, T 2,... T m, то дерево является упорядоченным (ordered tree).Если в упорядоченном дереве m>=2, то имеет смысл назвать поддерево Т2 вторым поддеревом данного корня и т.д. Упорядоченные деревья иногда также называются плоскими деревьями (plane treeы), поскольку при их упорядочении имеет значение способ размещения дерева на плоскости. Если не считать различными два дерева, которые отличаются только относительным порядком поддеревьев узлов, то дерево называется ориентированным (oriented), поскольку при этом имеет значение только относительная ориентация узлов, а не их порядок. Сама природа представления данных в компьютере определяет неявный порядок любого дерева, поэтому в большинстве случаев упорядоченные деревья представляют наибольший интерес.

Лес(forest) – это множество (обычно упорядоченное), содержащее несколько непересекающихся деревьев. Узлы дерева при условии исключения корня образуют лес. Между абстрактными понятиями леса и деревьев существует не очень заметная разница. При удалении корня дерева получим лес, и наоборот: при добавлении одного узла в лес, все деревья которого рассматриваются как поддеревья нового узла, получим дерево.Поэтому понятия лес и дерево часто используются как равнозначные при работе со структурами данных.

Путем из узла n 1 в узел n k называется последовательность узлов n 1, n 2, … n k, где для всех i, 1< i <k, узел n i является родителем узла n i +1. Длиной пути называется число, на единицу меньшее числа узлов, составляющего этот путь. Таким образом, путем нулевой длины будет путь из любого узла к самому себе. Например, на рисунке путем длины 2 будет путь от узла A к узлу F или от узла C к узлу G. Для рассмотрения деревьев необходимо создать описательную терминологию. Вместо двусмысленных формулировок лучше использовать общепринятые термины, которые применяются при работе с генеалогическими деревьями.Наиболее распространенные типы генеалогических деревьев- это родословная(показаны предки конкретного человека) и родовая схема(показаны наследники). Если существует путь из узла a в узел b, то в этом случае узел a называется предком узла b, а узел b – потомком узла a. Отметим, что любой узел одновременно является предком и потомком самого себя. Например, на рисунке предками узла G будут сам узел G и узлы F, C и A. Потомками узла C будут являться сам узел C и узлы D, T, F, G. В дереве только корень не имеет предков, а листья не имеют потомков.

Предок узла, имеющий уровень на единицу меньше уровня самого узла, называется родителем. Потомки узла, уровень которых на единицу больше относительно самого узла, называются сыновьями или детьми. Узлы, являющиеся сыновьями одного родителя, принято называть братьями.

Высотой узла дерева называется длина самого длинного пути от этого узла до какого-либо листа. Глубина узла определяется как длина пути от корня до этого узла.

Выше было упомянуто о родословной- и она является примером бинарного дерева - одного из наиболее важного типа деревьев. Каждый наверняка не раз встречался с бинарными деревьями в соревнованиях по теннису или других турнирах, которые проводятся по олимпийской системе с выбыванием проигравшего. Каждый узел бинарного дереваимеет не более двух поддеревьев, причем в случае только одного поддерева следует различать левое и правое. Строго говоря, бинарное дерево - это конечное множество узлов, которое является пустым или состоит из корня и двух непересекающихся бинарных деревьев, которые называются левым и правым поддеревьями данного корня. При работе с бинарными деревьями нужно не забывать об эпитете "бинарный", чтобы не путать их с обычными деревьями, так как бинарное дерево может быть пустым, а простое -нет. Древовидную структуру можно представть графически несколькими способами, которые могут выглядеть совершенно не так, как настоящие деревья в природе.

а)- вложенные множества б)вложенные скобки в)список с отступами

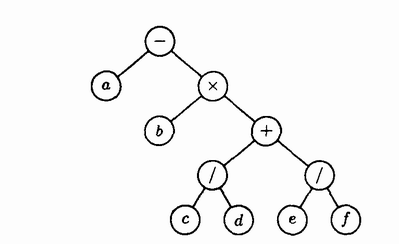
Еще одно изображение дерева, соответствующего арифметическому выражению а-b(c/d+e/f):

В свою очередь, лес можно рассматривать как особую структуру списка. Слово "Список" здесь применяется в очень специфическом смысле, и, чтобы подчеркнуть это, его пишут с прописной буквы. Рекурсивно Список определяется как конечная последовательность атомов или Списков, число которых может быть больше или равно нулю. здесь под словом "атом" подразумевается неопределенное понятие, которое может относиться к элементам любой совокупности объектов и которое можно отличить от Списка.С помощью обычной системы обозначений на основе запятых и скобок можно различать атомы и списки, а так же быстро и просто указывать упорядочение в пределах Списка. Рассмотрим список с 5 элементами L=(a,(b,a,b),(),c,(((2)))), в котором, сначала следует атом a, затем список (b,a,b), после, пустой Список (), атом с, и, наконец, Список(2). Последний Список состоит из списка ((2)), который включает список (2), который, в свою очередь, включает атом 2. Этому списку соответствует древовидная структура:

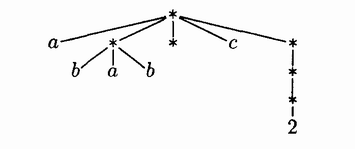
Звездочки используются для обозначения Списков, чтобы их можно было отличить от атомов. Индексные обозначения могут применяться для Списков точно так, как и для леса, например L[2]=(b,a,b) и L[2,2]=a. Узлы-Списки на схеме не несут никакой другой полезной информации, помимо того, что они являются Списками. Для устранения этого недостатка их можно пометить символами, как было сделано выше для деревьев и других структур. Важное отличие между Списками и деревьями заключается в том, что Списки могут перекрываться(подсписки могут пересекаться) и даже быть рекурсивными(содержать самих себя)

Четыре тесно связанных типа информационных структур -деревья, леса, бинарные деревья, Списки- имеют разное происхождение, поэтому они очень важны для компьютерных алгоритмов.

Обход бинарных деревьев Существует достаточно много алгоритмов работы с древовидными структурами, в которых наиболее часто встречается понятие "обхода"(traversing) дерева или прохода по дереву. При таком методе исследования дерева каждый узел посещается в точности один раз, а полный обход дерева задает линейное упорядочение узлов, что позволяет упростить алгоритм, так как при этом можно использовать понятие "следующий" узел, т.е.узел, который располагается перед данным узлом в таком упорядочении или после него. Для обхода бинарного дерева можно применить один из трех принципиально разных способов: в прямом порядке(preorder); в центрированном порядке(inorder); в обратном порядке(postorder); Эти три метода определяются рекурсивно.Если бинарное дерево пусто, то для его "обхода" ничего делать не потребуется, в противном случае обход выполняется в три этапа.

Прямой порядок обхода Попасть в корень Пройти левое поддерево Пройти правое поддерево

Центрированный порядок обхода Пройти левое поддерево Попасть в корень Пройти правое поддерево

Обратный порядок обхода Пройти левое поддерево Пройти правое поддерево Попасть в корень Эти три способа упорядочения узлов бинарного дерева в виде линейной последовательности чрезвычайно важны, поскольку они тесно связаны с большинством компьютерных методов обработки деревьев.Названия прямой, центрированный, обратный происходят,конечно, от расположения корня по отношению к поддеревьям. Во многих приложениях бинарных деревьев понятия левого и правого поддеревьев совершенно симметричны, и в таких случаях термин симметричный порядок используется в качестве синонима понятия центрированный порядок. Центрированный порядок, при котором корень располагается посередине, образует симметрию относительно левой и правой сторон: при отражении бинарного дерева относительно вертикальной оси получается простое обращение симметричного порядка.

Дата добавления: 2014-01-05