Однородное и изотропное случайное поле

При изучении случайных процессов весьма важным является условие стационарности, существенно упрощающее описание случайного процесса. Для пространственных полей аналогичными условиями являются условия однородности и изотропности. Случайное поле называется однородным, если все 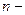мерные законы распределения не изменятся при переносе системы точек на один и тот же вектор, т.е. функции распределения (плотности распределения) не изменяются при замене сечений, соответствующих точкам 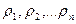сечениями, соответствующими точкам.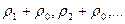При любом векторе .

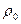Для однородного случайного поля математическое ожидание не зависит от координат точек поля, т.е. является постоянной величиной, а корреляционная функция зависит только от разности векторов .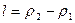

Случайное поле называется изотропным, если все его законы распределения не изменяются при всевозможных вращения систем точек вокруг любой оси, проходящей через начало координат, и при зеркальном их отражении относительно любой плоскости, проходящей через начало координат.

Таким образом, для однородного и изотропного случайного поля в широком смысле слова математическое ожидание есть величина постоянная, а корреляционная функция зависит только от модуля 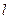. Значит, для однородного и изотропного случайного поля ).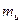

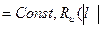Многочисленные исследования структуры метеорологических полей указывают на существенное различие изменений метеорологических элементов в горизонтальном и вертикальном направлениях. Поэтому при изучении мезо – и макромасштабных метеорологических полей свойства однородности относят только к горизонтальным координатам. При этом предполагается, что однородными являются только центрированные случайные поля. Само математическое ожидание нельзя считать постоянным.

Как и для стационарных случайных процессов, если однородное изотропное случайное поле обладает эргодическим свойством, его математическое ожидание и корреляционную функцию можно находить осреднением по одной реализации, заданной в достаточно большой пространственной области. В этом случае математическое ожидание определяется по формуле

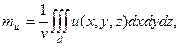(4.4)

где 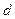- пространственная область, по которой производится осреднение, а 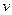- объем этой области.

Для плоского поля

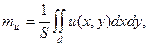(4.5).

где 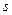- площадь плоской области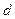

Для характеристики однородного и изотропного случайного поля наряду с корреляционной функцией используют и структурную функцию.

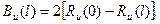(4.6)

Дата добавления: 2014-01-05