Правила перевода чисел из одной системы счисления в другую

· Перевод чисел из любой позиционной системы счисления с основанием q в десятичную систему счисления.

Перевод в десятичную систему числа х, записанного в q-ичной системе счисления (q=2,8 или 16) в виде x_q=(a_na_n-1…a₀,a_-1a_-2…a_-m)_q, сводится к вычислению значения многочлена

x₁₀=a_nqⁿ + a_n-1q^n-1+…+ a₀q⁰ + a_-1q^-1+ a_-2q^-2+…+ a_-mq^-m средствами десятичной арифметики.

1. Разряды 4 3 2 1 0

Число 1 1 0 1 1₂ = 1·2⁴ + 1·2³ + 0·2² + 1·2¹ + 1·2⁰ =27₁₀

2. Разряды 2 1 0 -1

Число 7 5 6, 1₈ = 7 · 8² + 5 · 8¹ + 6 · 8⁰ +1 · 8^-1=494,125₁₀

3. Разряды 2 1 0 -1

Число 2 4 7, 6₁₆ = 2 · 16² + 4 · 16¹ + 7 ·16⁰ + 6 · 16^-1 = 583,375₁₀.

4. Разряды 2 1

Число 1 B₁₆ = 1·16¹ +11 · 16⁰ = 27₁₀

· Перевод целого числа из десятичной системы в любую другую позиционную систему счисления.

Для перевода целого десятичного числа N в систему счисления с основанием q необходимо разделить N на q с остатком. Затем неполное частное, полученное от этого деления, нужно снова разделить на q с остатком и т.д. до тех пор, пока последнее полученное частное не будет меньше q. Результат записываем в обратном порядке, начиная с последнего частного и полученных остатков деления.

Перевести число 27₁₀ в двоичную, восьмеричную и шестнадцатеричную системы счисления.

27 / 2 = 13 и 1 в остатке; 13 / 2 = 6 и 1 в остатке; 6 / 2 = 3 и 0 в остатке; 3 / 2 = 1 и 1 в остатке; Ответ: 2710=110112=338=1В16.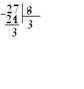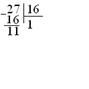

· Перевод правильной десятичной дроби в любую другую позиционную систему счисления.

Напомним, что правильная дробь имеет нулевую целую часть, т.е. у нее числитель меньше знаменателя (0,847). Результат перевода правильной дроби всегда правильная дробь.

Для перевода правильной десятичной дроби F в систему счисления с основанием q необходимо F умножить на q, записанное в той же десятичной системе, затем дробную часть полученного произведения снова умножить на q и т.д. до тех пор, пока дробная часть очередного произведения не станет равной нулю либо не будет достигнута требуемая точность изображения числа F в q-ичной системе. Результат записываем в виде последовательности целых частей полученных произведений, записанных в порядке их получения и изображенных одной q-ичной цифрой. Пример перевода числа 0,847 в 2-ую, 8-ую и 16-ую:

0,847	*2=	1,694	Целая часть
0,694	*2=	1,388	Целая часть
0,388	*2=	0,776	Целая часть
0,776	*2=	1,552	Целая часть	1 и т.д.
Ответ: 0,84710=0,11012

В данном примере процедура перевода прервана на четвертом шаге, поскольку получено требуемое число разрядов результата. Очевидно, это привело к потере ряда цифр.

0,847	*8=	6,776	Целая часть
0,776	*8=	6,208	Целая часть
0, 208	*8=	1,664	Целая часть	1 и т.д.
Ответ: 0,84710=0,66116

0,847	*16=	13,552	Целая часть
0,552	*16=	8,832	Целая часть
0,832	*16=	13,312	Целая часть	13 и т.д.
Ответ: 0,84710=0,D8D16

· Перевод дробных чисел (неправильных дробей) в любую другую позиционную систему счисления.

Неправильная дробь имеет ненулевую дробную часть, т.е. у нее числитель больше знаменателя (19,847). Результат перевода неправильной дроби всегда неправильная дробь.

При переводе отдельно переводится целая часть числа, отдельно – дробная. Результаты складываются.

· Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления и наоборот.

Перевод очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).

Пример:

5 3 7 1 1 А 3 F

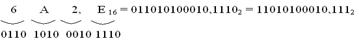
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой, при этом отбрасываются ненужные нули (крайние слева в целой части и крайние справа – в дробной).

Пример:

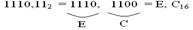
Дата добавления: 2014-01-05