Надежность расчлененных систем

При возможности расчленения сложной системы на отдельные неза­висимые элементы для расчета надежности широко используют струк­турные схемы. В этих схемах каждый i-й элемент характеризуется ве­роятностью его безотказной работы p_i в течение заданного периода времени и по этим значениям определяют вероятность безотказной ра­боты P (t) всей системы. Такие расчеты обычно называются расчетом схемной надежности.

Наиболее характерен случай, когда отказ одного элемента выводит из строя всю систему, как это имеет место, например, при последова­тельном соединении элементов (рисунок 2, а). Так, если в приводе машины откажет любой из его элементов - электродвигатель, редуктор, муфты, механизмы управления, насос смазки, то весь привод перестанет функ­ционировать. При этом отдельные элементы не обязательно должны быть соединены последовательно.

Рисунок 2 – Схема последовательного соединения элементов сложной системы

Вероятность безотказной работы такой системы равна произведению вероятностей безотказной работы элементов (по теореме умножения вероятностей независимых событий):

. (1)

При одинаковой надежности элементов формула (1) примет вид

. (2)

Сложные системы, состоящие из элементов высокой надежности, могут обладать низкой надежностью за счет наличия большого числа элементов. Например, если узел состоит всего из 50 деталей, а вероят­ность безотказной работы каждой детали за выбранный промежуток времени составляет p_i, = 0,99, то вероятность безотказной работы узла будет P (t) = (0,99)⁵⁰ = 0,55. Если же узел с аналогичной безотказно­стью элементов состоит из 400 деталей, то P (t) = (0,99)⁴⁰⁰ = 0,018, т.е. узел становится практически неработоспособным.

Для расчета надежности системы должен быть известен закон распределения сроков службы (наработки) для каждого элемента. Напри­мер, при внезапных отказах часто применяют экспоненциальный закон, в котором параметром является интенсивность отказов λ = const, и вероятность безотказной работы элементов определяется как

; …

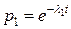Сделав подстановку в формулу (1), получим

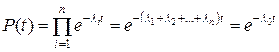. (3)

Таким образом, вероятность безотказной работы сложной системы в этом случае также подчиняется экспоненциальному закону с парамет­ром

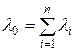. (4)

Простота подсчета надежности сложных систем при экспоненциаль­ном законе приводит часто к тому, что этим правилом пользуются и в тех случаях, когда причина выхода из строя – постепенный отказ с дру­гим законом распределения.

При расчете надежности системы необходимо учитывать, что зави­симость вероятности безотказной работы от времени p_i (_t) для каждого элемента, т.е. область состояния, формируется под влиянием процессов старения или внешних воздействий.

Схема формирования значения вероятности безотказной работы для системы с последовательно соединенными элементами показана рисунке 2, б.

Для каждого элемента характерна своя область состояний f_i (t), ко­торая может быть получена на основании расчета или с использованием статистических данных.

При изменении периода t = Т_р (ресурса), в течение которого рассматривается работа системы, изменяется и значение р_i для каждого элемента. Так, для изображенного на рисунке 2, б случая при увеличении ресурса от Т_{р 1} до Т_{р 2} вероятность отказа первого элемента возрастет в 2,5 раза, второй элемент станет практически неработоспособным (р ₂ = 0,5), а третий элемент по-прежнему не будет лимитировать зна­чение P (t) для всей системы.

Для повышения надежности сложных систем можно применять ме­тод резервирования, т.е. создавать дополнительные средства и возмож­ности для сохранения работоспособности системы при отказе одного или нескольких ее элементов. При резервировании ненадежных элемен­тов после отказа основного элемента дублер выполняет его работу, и узел продолжает функционировать. Резервирование может значительно повысить надежность системы.

Например, при постоянном (нагруженном) резервировании резерв­ные элементы постоянно присоединены к основным и находятся в оди­наковом с ними режиме работы (рисунок 3). Вероятность безотказной ра­боты P (t) системы, состоящей из основного и (m – 1) резервных эле­ментов, может быть подсчитана следующим образом. Пусть f ₁; f ₁;...; f_m – вероятности появления отказа каждого из m элементов за время t. Тогда отказ системы – это сложное событие, которое будет иметь место при условии отказа всех элементов, и вероятность совместного появле­ния всех отказов F (t) (по теореме умножения) составит

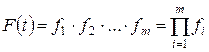. (5)

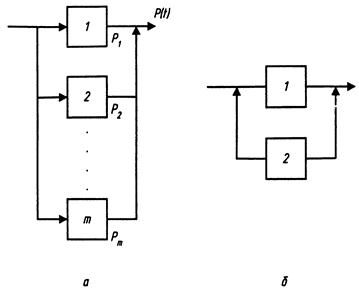
Рисунок 3 – Схема резервирования элемента: нагруженный (а) и ненагруженный дублирующий элемент (б)

Поэтому безотказность системы с параллельно резервированными элементами будет

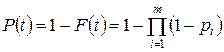. (6)

Например, если вероятность безотказной работы каждого элемента p = 0,9, а m = 3, то P (t) = l – (0,1)³ = 0,999. Таким образом, вероят­ность безотказной работы системы резко повышается и становится возможным создание надежных систем из ненадежных элементов.

Возможно также создание ненагруженного резервирования (резер­вирования замещением), когда резервные цепи находятся в отключен­ном состоянии и включаются лишь в том случае, если основная цепь или элемент отказывает (рисунок 3, б). Для обнаружения отказа необходим специальный прибор, а для включения резерва – соответствующее уст­ройство.

Таким образом, для нагруженного резерва надежность резервных элементов не зависит от того, в какой момент времени они включились вместо основного. Ненагруженные резервные элементы не работают до момента их включения вместо основного элемента, т. е. в этот период их отказ невозможен. Существует также облегченный резерв, когда резервные элементы до момента включения находятся в облегченном режиме работы и вероятность их отказа в этот период мала.

Академик Б.В. Гнеденко, рассматривая облегченный резерв как об­щий случай резервирования, дает метод для оценки вероятности отказа резервированного элемента. Достаточно простой метод расчета по­лучается лишь при экспоненциальном законе.

Если все элементы (основной и резервные) одинаковы и λ ₁ – интен­сивность отказов в облегченном режиме, а λ – в рабочем, то при высо­ких значениях вероятности безотказной работы элементов получена следующая приближенная формула:

. (7)

Исследованию различных видов резервирования посвящена обшир­ная литература.

Рассматривая систему, состоящую из n последовательно соединен­ных элементов, можно предложить несколько вариантов их резервиро­вания.

Общее резервирование (рисунок 4, а), когда при выходе из строя любо­го элемента включается резервная цепь, которая полностью заменяет данную. Имеется (m – 1) резервных цепей (всего m цепей).

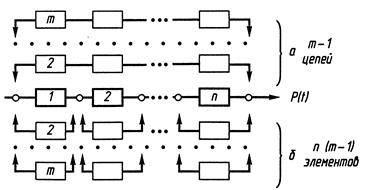
Рисунок 4 – Схема общего (а) и раздельного (б) резервирования системы

Если p_i – вероятность безотказной работы одного элемента, a P_j – всей цепи, то безотказность системы Р ₀, согласно формулам (6) и (1), будет

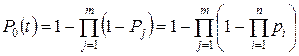. (8)

При одинаковых по безотказности элементах (р_i = р ₁) формула (8) примет вид

. (9)

Например, при n = 4, m = 3 и p_i =0,9 Р ₀ = 1 – (1 – 0,9⁴)³ = 0,958.

Раздельное резервирование (рисунок 4, б), при котором имеется возможность включать резервный элемент при выходе из строя любого элемента, значительно повышает надежность системы.

В этом случае вероятность безотказной работы системы вычисляется по формуле

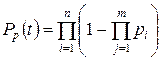. (10)

При одинаковых элементах формула (10) примет вид

. (11)

Используя данные из приведенного выше примера, получим Р_р = (1 – 0,1³)⁴ =(0,999)⁴, что соответствует высокому уровню безот­казности системы.

Следует, однако, отметить, что раздельное резервирование приводит к усложнению всей системы, что снижает эффект от ее применения.

На практике часто применяют смешанные системы резервирования с общим резервированием отдельных цепей и раздельным резервирова­нием наиболее ответственных и менее надежных элементов. Сравнение вариантов резервирования с точки зрения безотказности системы про­водится аналогичными методами. В радиоэлектронных системах нахо­дят применение более разнообразные методы резервирования, напри­мер, скользящий резерв, когда дублирующий элемент может заменить любой основной элемент в данной группе или избирательное резерви­рование (по «схеме голосования»), когда выходной параметр для парал­лельных цепей формируется на основании сравнения сигналов на выхо­де каждой из цепей. Однако такие методы не являются характерными для машиностроения.

При расчете схемной надежности следует иметь в виду, что конст­руктивное оформление элементов, их последовательное или параллель­ное соединение при монтаже еще не означает аналогичного изображе­ния в структурной схеме.

Разница между конструктивной (монтажной) и структурной схемами показана на рисунок 5 на примере двух фильтров гидросистемы, которые для повышения надежности работы системы могут быть установлены последовательно или параллельно. Отказ фильтра может произойти в результате засорения сетки или ее разрыва.

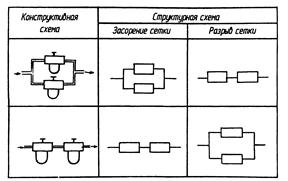
Рисунок 5 – Конструктивные и структурные схемы соединения фильтров при различных видах отказов

В случае засорения сетки структурная схема соответствует конст­руктивной, и последовательное соединение фильтров в этом случае только снизит надежность системы, так как отказ любого из фильтров приведет к отказу системы (необходимый поток жидкости не будет проходить сквозь фильтр).

При отказе фильтра из-за разрыва сетки структурная схема противо­положна конструктивной. При параллельном конструктивном выполне­нии отказ любого фильтра будет означать отказ системы, так как при разрыве сетки неочищенный поток жидкости пойдет через данный фильтр. Поэтому структурная схема изображена в виде последователь­ных элементов. При последовательном конструктивном включении фильтров наоборот разрыв сетки одного из них не будет означать отка­за, поскольку дублирующий фильтр продолжает выполнять свои функ­ции. Поэтому структурная схема изображена в виде параллельного со­единения.

При расчете схемной надежности необходимо предварительно иметь данные о надежности каждого элемента. Пусть, например, для простей­шей системы из четырех звеньев (это может быть частью более сложной системы) известны значения вероятности безотказной работы каждого звена (рисунок 6, а), которые равны р ₁ = 0,99; р ₂ = 0,9; р ₃ = р ₄ = 0,98. Тогда вероятность безотказной работы этой системы, подсчитанная по формуле (1), будет равна 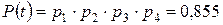. Если необхо­димо повысить надежность системы без изменения качества самих элементов, то это можно сделать за счет дублирования второго элемента, надежность которого значительно ниже остальных элементов (рисунок 6, б). В этом случае вероятность безотказной работы основного и резервного элементов № 2 и № 2' по формуле (6) будет

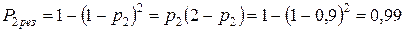. (12)

Таким образом, надежность резервированного элемента на порядок выше, чем у каждого из пары. Поэтому безотказность работы всей сис­темы возрастет и станет равной

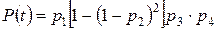или 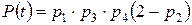, (13)

т.е. .

Для сложных систем обычно просчитывают аналогичным образом различные варианты соединения и резервирования и выбирают опти­мальное решение.

Для систем, в которых имеют место более сложные функциональные связи, чем последовательное или параллельное соединения элементов, можно использовать формулу полной вероятности (формула Байеса) для оценки безотказности их работы.

При анализе надежности сложных структур находит применение метод логических схем с использованием алгебры логики (алгебры Бу­ля).

Логические схемы иногда получаются громоздкими, однако, они применимы к более широкому кругу систем.

Анализ схемной надежности в этом случае основывается на форму­лировании условия безотказности, используя символы и правила алгеб­ры логики. Рассмотрим в качестве примера расчет схемы, приведенной на рисунке 6, в. Безотказность работы элемента обозначим символом А с соответствующим индексом, а противоположное ему событие (отказ) – символом .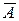

Рисунок 6 – Схема для расчета системы из четырех элементов методом структурных (а, б) и логических (в) схем

Сложное событие, заключающееся в выполнении каждого из состав­ляющих его событий, будет их логическим умножением («И»), а воз­никновение одного из них – логическим сложением («ИЛИ»).

В символах алгебры логики сложное событие В – безотказность ра­боты системы (см. рисунок 6 б, в) – выразится как

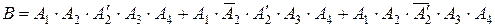. (14)

Эта запись формулирует три варианта безотказной работы системы, когда работают все элементы, или все, но с отказом основного (№ 2), или все, но с отказом резервного (№ 2'). Заменив события их вероятно­стями и считая р ₂ = р '₂, получим уравнение для определения вероятно­сти безотказной работы системы:

Таким образом, получили ту же формулу, что и выше (формула 13).

Иногда считают, что метод расчета структурных схем для определе­ния вероятности безотказности систем и выбор оптимального варианта является чуть ли не основным при оценке надежности сложного изде­лия. В действительности основная трудность заключается не столько в методах расчета структурных схем, сколько в оценке и прогнозирова­нии значений надежности отдельных элементов, в определении законов изменения выходных параметров в функции времени и в других зада­чах. Кроме того, применимость структурных схем для механических систем и изделий более ограничена, чем для радиоэлектронных систем.

Рассматривать формирование показателей надежности машин и ме­ханических систем в виде расчлененных структур можно в большинстве случаев весьма условно и, как правило, лишь тогда, когда к их выход­ным параметрам не предъявляются достаточно жесткие требования, а необходимо обеспечить функционирование отдельных узлов и меха­низмов системы.

Чем совершеннее изделие и чем выше требования к его параметрам, тем в большей взаимосвязи находятся все элементы системы. Разбивать систему на независимые элементы и применять формулы для расчета P (t) расчлененных систем можно для механических систем и машин в следующих основных случаях:

• при рассмотрении больших систем, состоящих из отдельных ма­шин, самостоятельных агрегатов и подсистем (например, технологические комплексы);

• при рассмотрении нескольких независимых выходных параметров изделия;

• при анализе надежности машин, состоящих из отдельных агрега­тов, особенно в тех случаях, когда их принцип работы и особенность функционирования представляют самостоятельную конст­руктивную единицу (узлы гидросистем, двигатели и агрегаты са­молета, целевые узлы станков - коробка скоростей, механизм за­
грузки и подачи и другие).

Все перечисленные случаи условны и требуют предварительного анализа для решения вопроса о возможности расчленения изделия на независимые элементы и подсистемы.

В общем случае оценка схемной надежности более пригодна для оп­ределения надежности функционирования изделия, а рассмотрение схемы со связанными элементами характерно для определения пара­метрической надежности.

Дата добавления: 2014-01-05