Введение. На предыдущих лекциях мы ознакомились с различными типами уравнений регрессии (парной и множественной) и убедились в том

ТЕКСТ ЛЕКЦИИ

На предыдущих лекциях мы ознакомились с различными типами уравнений регрессии (парной и множественной) и убедились в том, что в зависимости от того, сколько и каких именно факторных переменных будет включено в уравнения регрессии, может существенно зависеть результат расчетов. В практических расчетах нельзя использовать уравнения регрессии, параметры которых оценены недостаточно точно, а сами уравнения недостаточно адекватно описывают реальную статистическую зависимость между переменными. Поэтому при построении и анализе построенных эконометрических моделей особое место уделяется анализу их значимости (или существенности). Различные методы оценки значимости построенных моделей и их отдельных параметров мы рассмотрим на данной лекции.

1й учебный вопрос. Проблема оценки значимости уравнений регрессии

Как уже выяснилось из предыдущих лекций, уравнение парной линейной регрессии представляет собой функциональную связь, при которой по любому значению переменной х можно однозначно определить значение переменной у. Функциональная связь лишь приближенно отражает связь реальную, причем степень этого приближения может быть различной и зависит она как от свойств исходных данных, так и от выбора вида функции, по которой производится выравнивание исходных статистических данных.

Однако с помощью одного и того же уравнения регрессии можно теоретически описать совершенно разные варианты соотношений между признаками x и y. В одном случае исходные статистические данные, если изобразить их на графике поля корреляции, будут достаточно близко располагаться от прямой линии. В другом случае, они будут довольно сильно разбросаны. В первом случае соотношение между признаками х и у достаточно четко выражено, и уравнение парной линейной регрессии, по-видимому, довольно хорошо описывает это соотношение, тогда как во втором случае сомнительно само наличие сколько-нибудь закономерного соотношения между признаками.

И в том, и в другом случаях, несмотря на их существенное различие, метод наименьших квадратов даст одинаковое уравнение регрессии, поскольку этот метод нечувствителен к потенциальным возможностям исходного материала вписаться в ту или иную схему. Кроме того, метод наименьших квадратов применяется для расчета неизвестных параметров заранее выбранного вида функции, и вопрос о выборе наиболее подходящего для конкретных данных вида функции в рамках этого метода не ставится и не решается. При использовании метода наименьших квадратов открытыми остаются два важных вопроса, а именно: 1) существует ли вообще статистическая связь и 2) верен ли выбор вида функции, с помощью которой делается попытка описать форму связи.

Чтобы оценить, насколько точно уравнение регрессии описывает реальные соотношения между переменными, нужно ввести меру рассеяния фактических значений относительно вычисленных с помощью уравнения. Такой мерой служит, в частности, средняя квадратическая ошибка (ошибка аппроксимации) регрессионного уравнения, вычисляемая по хорошо известной формуле (как квадратный корень из суммы квадратов остатков (т.е. отклонений расчетных значений от фактических), деленной на длину исходного ряда данных.

Подобно тому, как по величине среднего квадратического отклонения можно судить о представительности средней арифметической, по величине средней квадратической ошибки регрессионного уравнения можно сделать вывод о том, насколько показательна для соотношения между признаками та связь, которая выявлена уравнением. В каждом конкретном случае фактическая ошибка может оказаться либо больше, либо меньше средней. Средняя квадратическая ошибка уравнения показывает, насколько в среднем мы ошибемся, если будем пользоваться уравнением, и тем самым дает представление о точности уравнения. Чем меньше σ_yx, тем точнее предсказание линии регрессии, тем лучше уравнение регрессии описывает существующую связь.

Варьируя виды функций для выравнивания и оценивая результаты с помощью средней квадратической ошибки, можно среди рассматриваемых выбрать лучшую функцию, функцию с наименьшей средней ошибкой.

Но существует ли сама связь? Является ли значимым уравнение регрессии, используемое для отображения предполагаемой связи? На эти вопросы отвечает лучше всего определяемый ниже критерий Фишера.

Под значимостью или существенностью уравнений регрессии в эконометрике обычно понимается – степень адекватного учета реальных статистических данных и взаимосвязей значений отдельных показателей в конкретном уравнении регрессии.

Для оценки значимости принято использовать несколько основных показателей. Рассмотрим их по порядку.

Во-первых, это уже хорошо известная нам ошибка аппроксимации (характеризующая степень отклонений расчетных значений 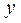от фактических). Ошибка аппроксимации рассчитывается по формуле средней квадратической, то есть представляет собой среднее квадратическое отклонения расчетных и фактических значений результативной переменной:

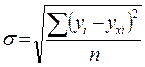
где

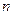– число наблюдений

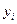– фактическое значение

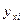– расчетное значение, которое определяется по формуле:

…

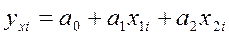Во-вторых, это дисперсия расчетных значений 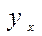то есть:

,

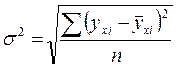где средняя величина расчетных значений на самом деле всегда совпадает со средней величиной фактических значений, так как метод наименьших квадратов «устроен» так, что всегда обеспечивает совпадение сумм расчетных и фактических значений результативной переменной.

– средняя расчетных значений

В-третьих, это уже хорошо известный нам индекс детерминации, который рассчитывается как отношение дисперсии расчетных значений к дисперсии фактических:

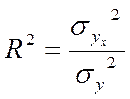
При этом дисперсия фактических значений рассчитывается по формуле:

В-четвертых, это коэффициент множественной корреляции, который определяется как квадратный корень из индекса детерминации, но принципиально может быть рассчитан и другими способами.

=

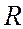Дата добавления: 2014-01-05