Функция двух переменных

Определение. Переменнаяz называется функцией двух независимых переменных х и у из некоторого множества D, если каждой точке 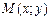из D по некоторому правилу ставится в соответствие одно определенное значение z.

Обозначение: 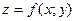или . Множество D называется областью определения функции z.

Частные производные. Пусть 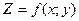− функция двух переменных. Если зафиксировать один из аргументов, 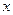или 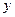, то получим функцию одной переменной.

Частной производной первого порядка функции 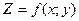по какой-либо переменной называется обычная производная функции , вычисленная при условии, что другая переменная остается неизменной.

Частные производные обозначаются так:

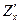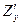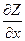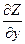, или , , или , .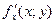

Частные производные первого порядка функции 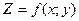, вообще говоря, являются функциями двух переменных 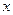или 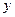, поэтому для них также можно найти частные производные, которые называются частными производными второго порядка.

, , , .

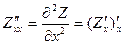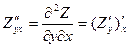Частные производные и 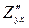отличающиеся порядком дифференцирования, называются смешанными частными производными второго порядка. Если смешанные частные производные второго порядка непрерывны, то .

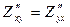Полным приращением функции 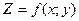называется величина

.

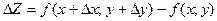Полным дифференциалом функции 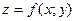называется выражение

.

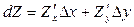Так как 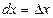, , 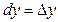дифференциал 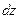можно записать в виде . При достаточно малых значениях 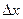и .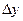

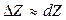Дата добавления: 2014-01-05