Закон Кулона

Многочисленными экспериментами различных авторов установлено, что график зависимости сопротивления сдвигу от нормального напряжения для песчаных и крупнообломочных грунтов в интервале изменения а, представляющем интерес для промышленного и гражданского строительства (до 0,3...0,5 МПа), с достаточной точностью может быть представлен отрезком прямой, выходящей из начала координат (рис. 7.2, б). Тогда эта зависимость может быть выражена уравнением

τ_пр = σtg φ = σf (7.1)

Поскольку сопротивление сдвигу сыпучих (песчаных и крупнообломочных) грунтов определяется прежде всего сопротивлением трению перемещающихся частиц, угол φ принято называть углом внутреннего трения, а коэффициент пропорциональности f = tg φ — коэффициентом внутреннего трения сыпучего грунта.

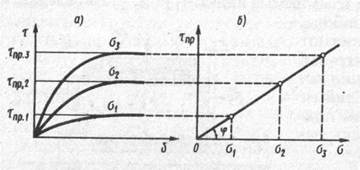
Рис. 7.2. Кривые горизонтальных перемещений образцов при различных значениях σ (а) и график сопротивления сдвигу образцов песчаного грунта (б)

Проведя подобные испытания для образцов глинистых грунтов, получают более сложную криволинейную зависимость (рис. 7.3). Здесь сопротивление сдвигу обусловливается не только силами трения, возникающими между перемещающимися частицами, но и связностью грунта, т. е. сложными процессами нарушения пластичных (водно-коллоидных) - и более жестких (цементационных) связей. Однако, как для сыпучих грунтов, зависимость сопротивления сдвигу от нормального напряжения обычно представляется в виде уравнения отрезка прямой

τ_пр = σtg φ + c = σf +c. (7.2)

Отрезок с, отсекаемый на оси τ этой прямой, называется удельным сцеплением глинистого грунта и характеризует его связность.

Параметры φ и с лишь условно могут быть названы углом внутреннего трения и удельным сцеплением, так как физика процесса разрушения грунта значительно сложнее. На самом деле это всего лишь параметры зависимости данного грунта, полученные опытным путем. Однако такое их наименование сложилось исторически и широко используется в механике грунтов. Отметим также, что при определенных условиях даже сыпучие грунты могут обладать некоторой «связностью». Например, влажные пески, особенно мелкие и пылеватые, под действием капиллярно-стыковой воды приобретают небольшую связность. При сдвиге крупнообломочных грунтов и крупных песков, особенно однородных, за счет зацепления частиц также могут возникать относительно небольшие значения удельного сцепления. Однако силы связности в этих случаях очень малы и не оказывают существенного влияния на сопротивление сдвигу.

Уравнения (7.1) и (7.2) часто называют законом Кулона для сыпучих и связных грунтов, формулируя этот закон в таком виде: сопротивление грунтов сдвигу есть функция первой степени от нормального давления.

Обычно при использовании этих уравнений индекс «пр» (предельное) при τ опускают, имея в виду, что они справедливы только в предельном состоянии. Очевидно, что чем больше при равных σ значения параметров φ и с, тем более прочным является данный грунт.

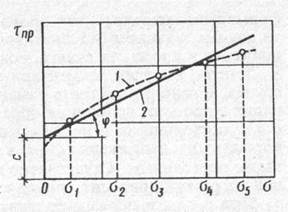
Рис. 7.3. График сопротивления сдвигу образцов глинистого грунта

1 – опытная кривая; 2 – спрямленный график

Дата добавления: 2014-01-05