Вычисление произведения элементов чисел

Вычисления произведения элементов массива осуществляется с помощью функции и , где 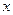- вектор или матрица элементов. Если 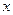- вектор, то функция вычисляет произведение элементов вектора. Если 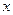- матрица, то откликом будет вектор, элементами которого являются произведение каждого столбца матрицы.

Функция дополнительно возвращает частичные произведения элементов вектора или столбца матрицы.

Пример.

Необходимо вычислить:

♦ произведение чисел от1 до 10;

♦ произведение элементов вектора [1,4,9,16,25];

♦ произведение квадратов элементов вектора [1,4,9,16,25];

♦ частичные произведения столбцов матрицы [1,2,3,4;2,3,4,5;3,4,5,6;4,5,6,7].

Решение:

1.>> x=1:10;

>> P=prod(x)

P = 3628800

2.>> x=[1,4,9,16,25];

>> P=prod(x)

P = 14400

3.>> x=[1,4,9,16,25].^2;

>> P=prod(x)

P = 207360000

4.>> x=[1,2,3,4,;2,3,4,5;3,4,5,6;4,5,6,7];

>> P=prod(x)

P = 24 120 360 840

5.>> P=cumprod(x)

P = 1 2 3 4

2 6 12 20

6 24 60 120

24 120 360 840

Вычисление пределов в среде MATLAB.

В MATLAB пределы вычисляются с помощью функции limit (f, x, x0), где:

f - функция, предел которой определяется;

x - аргумент функции f;

х0- предельное значение х.

Технология вычисления пределов:

1. Определение символьной переменной с помощью функции syms x.

2. Ввод функции limit(f, x, x0).

3. Получение решения после нажатия клавиши <Enter>.

Наиболее часто пределы вычисляются при х→ 0 или при х→ ∞. Символ ∞ кодируется в MATLAB словом inf.

Системы компьютерной алгебры позволяют находить пределы функции, в том числе и в случаях, когда имеют место неопределенности вида [∞/∞], [0/0], [0*∞], [∞ - ∞], [1].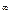

Пример. Вычислить пределы следующих функций:

>> syms x

1) >> limit((x^3+5*x^2+8*x+4)/(x^3+7*x^2+16*x+12),x,-2)

ans = -1

Ответ: -1

2) >> limit(((2*x-1)/(2*x+3))^(4*x+1),x,inf)

ans = exp(-8)

Ответ: e

Функция limit находит предел функции в некоторой точке, включая и плюс или минус бесконечность. Первым входным аргументом limit является символическое выражение, вторым - переменная, а третьим - точка, в которой разыскивается предел.

Пусть, например, требуется вычислить

Для получения ответа определите и 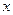, как символические переменные, и используйте inf в качестве точки предела:

>> syms a x

>> limit((1+1/x)^(x*a),x,inf)

ans =exp(a)

Функция limit позволяет находить односторонние пределы, для нахождения предела справа следует указать четвертый дополнительный аргумент ' right ', а слева – ' left '.Найдите решение следующих двух задач

; .

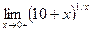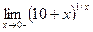Очевидно, что следует выполнить следующие команды:

1>> syms b x

>> limit((10+x)^(1/x),x,0,'left')

ans =0

2>> limit((10+x)^(1/x),x,0,'right')

ans =inf

Обратите внимание, что обычный предел в точке ноль в предыдущем примере не существует:

3>> limit((10+x)^(1/x),x,0)

ans =NaN

Дата добавления: 2014-01-05