Деформационные свойства

МЕХАНИЧЕСКИЕ СВОЙСТВА ПОЛИМЕРОВ

Механические свойства определяют степень изменения структу­ры, размеров, формы тела при воздействии на него механичес­ких сил. В зависимости от величины и продолжительности действия механических сил полимерные материалы подверга­ются деформации или разрушению. Соответственно различают деформационные и прочностные свойства. Деформационные свойства характеризуют способность полимерных материалов деформироваться под воздействием механических напряжений, прочностные – способность сопротивляться разрушению.

Вследствие специфики строения макромолекул и надмолеку­лярных структур механические свойства полимеров характери­зуются рядом особенностей и сильно зависят не только от сос­тава и строения полимера, но и от внешних условий. Работоспо­собность полимерных материалов во многом определяется ре­жимом их деформирования, прежде всего характером действия внешних сил. Различают статические и динамические режимы нагружения. К статическим относят воздействия при постоян­ных нагрузках или деформациях, а также при небольших ско­ростях нагружения, к динамическим – ударные или цикличес­кие воздействия.

Деформацией тела называется изменение его размеров, объема и формы под влиянием температуры, внешнего механического воздействия или внутренних сил. Деформация сопровождается изменением структуры полимеров и их свойств: чем сильнее деформация, тем значительнее изменение структуры и свойств.

Степень деформации оценивается относительной деформацией ε, равной отношению абсолютной деформации ∆l к размеру образца l до деформа­ции:

ε =∆l / l

Величина деформирующих сил характеризуется напряжением, т.е. силой, приходящейся на единицу площади сечения тела. Различают истинное σ и условное f напряжения при деформации:

;

где Р – деформирующая сила; S_ε, S_o – площади поперечных сечений при де­формации ε и до нагружения.

Эти показатели связаны соотношением:

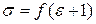
Можно выделить три вида деформации: простой сдвиг, одноосное растяжение, всестороннее сжатие (или растяжение) (рис. 5.1).

При простом сдви­ге деформирование происходит под действием тангенциальных (касательных) напряжений σ_τ, действующих на поверхности образца. При этом изменяется форма образца, а объем остается постоянным. Деформация сдвига γ опреде­ляется тангенсом угла α при сдвиге верхней плоскости АВ относительно нижней 00' в положение А'В', т.е. тангенсом угла поворота α прямой ОА (ОА – расстояния между плоскостями). Модуль сдвига G= σ_τ/ γ. Скорость сдвига представляет собой величину, характеризующую изменение деформации во времени.

Одноосное растяжение происходит под действием нормальных напряже­ний σ_н, приложенных перпендикулярно поверхности образца. При этом наблю­даются продольное растяжение ε_прод и поперечное сжатие образца ε_попер. Степень растяжения λ равна отношению длин образца после (l) и до (l₀) растяжения: λ= l/l₀

Относительное удлинение при растяжении ε_прод равно:

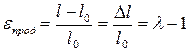
Модуль при одноосном растяжении Е (модуль Юнга) равен:

Мерой поперечного сжатия при одноосном растяжении является безраз­мерная величина – коэффициент Пуассона μ=ε_попер/ ε_прод.

Обычно для эластомеров μ=0,48÷0,49, для пластмасс μ =0,2÷0,4.

Если до деформирования образец имел размеры а, Ь, с, а после – х, y, z, то степень деформирования составит

λ₁=x/a; λ₂=y/b; λ₃=z/c

Если объем тела не изменяется при деформировании, то abc=xyz и λ₁λ₂λ₃ = 1.

При всестороннем сжатии (растяжении) под действием нормальных напряжений происходит изменение объема образца, а форма не изменяется. В этом случае сжимающим напряжением является давление Р. Объемная деформация ε_об в равна относительному изменению объема ∆V/V. Модуль всестороннего сжатия К равен:

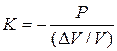
при растяжении Е, сдвиге G и всестороннем сжатии К связаны соотношением:

Податливость (величина, обратная модулю) при простом сдвиге равна J= 1 /G, при всестороннем сжатии В= 1 /К, при растяжении D =1/ E.

Деформационные свойства полимеров обычно оценивают по кривым напряжение – деформация (σ–ε). На рис. 5.2 приведены диаграммы растяжения для различных полимеров. Нес­мотря на разный характер кривых, на всех можно выделить начальный участок до точки А, где наблюдается линейная за­висимость между σ и ε, т. е. выполняется закон Гука, выве­денный для твердых тет: σ = Е ε, где Е – модуль упругости (мо­дуль Юнга), численно равный σ при ε = 1. т.е. при изменении линейного размера в два раза. Напряжение, соответствующее точке А, называют пределом упругости σ_упр, а деформацию – упругой ε_упр.

При дальнейшем нагружении при σ > σ_упр (точка А) закон Гука уже не выполняется. В общую деформацию таких систем, кроме упругой составляющей ε_упр входят высокоэластическая ε_эл и вязкотекучая ε_вт:

ε= ε_упр+ ε_эл+ ε_вт

Относительный вклад каждого вида деформации определя­ется условиями деформирования (температура, скорость), фи­зическим и фазовым состоянием полимера и его структурой.

На ход кривой σ–ε оказывает влияние и релаксационный характер деформации, наиболее ярко проявляющийся в высокоэластическом и вязкотекучем состояниях. Релаксационный характер проявляется в отставании деформации от напряжения при деформировании и наличии остаточных деформаций после снятия нагрузки. Относительная остаточная деформация равна 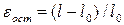, где l – длина образца после снятия нагрузки.

Иногда по величине ε_ост полимеры делят на пластичные и эластичные. Пластичные сохраняют приданную им деформа­цию (форму) послe удаления деформирующей силы и ε_ост=ε, эластичные – восстанавливают размеры и форму до начальных. В этом случае ε_ост→0. Скорость восстановления определяется скоростью релаксации и зависит от структуры, физического и фазового состояния полимера.

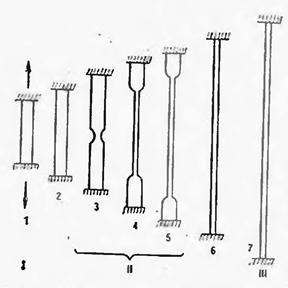Деформационные свойства стеклообразных полимеров. На рис 5.3 приведена характерная кривая (1) σ–ε стеклообразно­го полимера, а на рис. 5.4 схематически изображены стадии де­формирования при растяжении.

Процесс деформирования мож­но разделить на три стадии. На стадии I до точки А полимер деформируется упруго, соблюдается закон Гука (напряжение пропорционально деформации, форма образца практически не изменяется). Деформационные свойства оцениваются модулем упругости Е и упругой деформацией ε_упр. В точке А (см. рис. 5.3) начинается стадия II, характеризующаяся сильным растяжением образцов при незначительном росте напряжения. Если сопоставить этот участок деформационной кривой с кри­вой установившегося течения (см. рис 4.8), то можно провести аналогию между этими процессами. Поэтому деформацию стеклообразного полимера на II участке называют «холодным» течением. В начале этой стадии в точке В напряжение несколь­ко снижается и образец утончается, возникает так называемая «шейка» и дальнейшее растяжение образца происходит только за счет удлинения «шейки» Длина «шейки» растет до тех пор, пока она не распространится на всю растягиваемую часть об­разца, причем толщина «шейки» на стадии II остается посто­янной. В точке С весь образец переходит в «шейку» и начи­нается III стадия растяжения. Образец в виде «шейки» растягивается по всей длине равно­мерно (вплоть до разрыва в точке D), при этом напряжения вновь возрастают практически пропорционально удли­нению.

Таким образом, для стадий I и III характерна невысокая обратимая упругая деформация. Деформация, достигнутая на II стадии, сохраняется после снятия нагрузки, но она не является истинно пластичной. Если образец с «шейкой» нагреть ил подвергнуть набуханию (т. е. ускорить релаксацию), то «шейка» исчезнет и образец примет первоначальную форму. Это свидетельствует о том, что деформация на II стадии высокоэластическая. В отличие от обычной высокоэластичности, проявляемой при Т>Т_с, подобная высокоэластичность при Т<Т_с, для проявления которой недостаточно энергии тепловой движения, а требуется действие больших напряжений, называется вынужденной высокоэластичностью, деформации – вынужденно-эластическими ε_в, а напряжение, при котором начинает проявляться вынужденная высокоэластичность, – пределом вынужденной высокоэластичности σ_в.

Кривая 1, приведенная на рис. 5.3, является полной деформационной кривой стеклообразного полимера, однако часто образец разрывается на II или I стадиях – в этом случае говорят о неполной деформационной кривой (кривые 2, 3).

Механизм образования «шейки», т. е. «холодной» вытяжки объясняется с различных точек зрения. На первой стадии упругое деформирование (по связям и углам) сопровождается увеличением свободного объема. Полимер по своей структуре неоднороден, в нем существуют слабые (дефектные) и более прочные участки. При нагружении дефекты структуры являются концентраторами напряжения, поэтому в полимере происходят локальные микроразрывы цепей, приводящие к образованию микротрещин и микропустот размером ≈2÷20 нм, которые способствуют увеличению свободного объема.

Рост свободного объема обусловливает возможность изме­нения конформации под действием напряжения и переход в ориентированное состояние, т. е. полимер проявляет способность к высокоэластическому деформированию, для которого характерны релаксационные явления. Безусловно, высокое напряжение в дефектном участке релаксирует и распределяется на другие участки. Релаксации напряжения способствуют микропустоты. Таким образом, релаксационными явлениями можно объяснить некоторое снижение σ после точки А.

Нельзя не учитывать и изменение активационного барьера вращения атомов и их групп вокруг одинарных связей при наложении напряжения. Прикладываемое напряжение умень­шает потенциальный барьер, ограничивающий сегментальную подвижность, и увеличивает вероятность движения в направле­нии приложенной силы, т. е. увеличивается вероятность течения («холодной» вытяжки).

Уменьшение потенциального барьера влечет за собой и ус­корение релаксации. Время релаксации τ^* определяется не только температурой [см. уравнение (4.47)], но и напряжени­ем:

(5.1)

где α – константа.

При малых напряжениях (ασ<<U₀) урав­нение (5.1) переходит в уравнение, описывающее релаксацию под влиянием теплового движения. В стеклообразном состоянии U₀>>kT и величина τ^* велика. При больших σ (ασ → U₀) вре­мя релаксации снижается и макромолекулы способны изменить конформацию, т.е. способны проявить высокоэластическую де­формацию.

После перехода всего полимера в ориентированное состоя­ние (III участок) в системе значительно возрастает уровень межмолекулярного взаимодействия, т. е. плотность физичес­кой сетки, за счет сближения цепей. Внутреннее сопротивление деформированию у таких систем велико, и они ведут себя как твердые тела

Предел вынужденной эластичности σ_в снижается с ростом температуры или с уменьшением скорости деформирования, а величина деформации растет. При снижении температуры на­пряжение σ_в, необходимое для реализации вынужденной высокоэластичности, повышается. При какой-то температуре σ_в достигает значения, при котором происходит хрупкое разрушение полимера, т.е. σ_в=σ_хр. Эта температура назы­вается температурой хрупкости Т_хр. При этой температуре кривая σ–ε становится неполной (см. рис. 5.3, кривая 3) и полимер разрушается хрупко: точки А и D совпадают; Т_хр, так же как и Т_с, является неравновесной характеристикой, за­висит от скорости нагружения и вида деформации (сжатие, растяжение, сдвиг).

На рис. 5.5 представлены зависимости σ_хр и σ_в от температуры для трех полимеров, имеющих одинаковую Т _с.

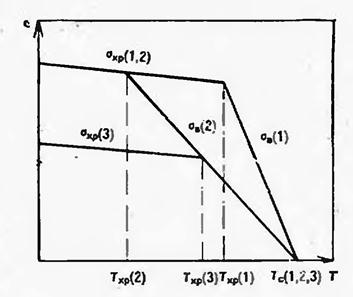
Полимеры 1 и 2 характеризуются оди­наковой σ_хр, но разным тем­пом изменения σ_в с темпе­ратурой [(d σ_в /dT)₁>> (d σ_в /dT)₂ ]. Поэтому Т_хр (1) выше Т_хр (2). Поли­мер 3 имеет такой же темп изменения σ_в с температурой, но меньшую σ_хр, поэтому Т_хр (3) > Т_хр (2). Как видно из рис. 5.5, ∆Т_в=Т_с – Т_хр зависит от разрушающего напряжения при хрупком разрыве σ_хр и темпа изменения σ_в с температурой (d σ_в /dT) при одинаковой Т_с.

Рассмотрим в качестве примера полистирол (Т_с = 373 К) и полиметилметакрилат (Т_с = 383 К). Из-за низкого значения σ_хр и большой скорости роста σ_в с температурой полистирол имеет более высо­кую Т_хр и меньший интервал вынужденной высокоэластичности ∆Т_в, чем полиметилметакрилат (рис.5.6). Поэтому полисти­рол нельзя использовать в изделиях, для которых требуется вы­сокая стойкость к ударным нагрузкам (ударная вязкость).

Для расширения ∆Т_в полимеры модифицируют эластомерами, гиб­кие макромолекулы которых способствуют ускорению релаксационных процессов и сдвигают Т_хр в сторону меньших значе­ний, повышая ударную вязкость.

Температура хрупкости снижается с уменьшением плотнос­ти упаковки и ростом молекулярной массы. При рыхлой упа­ковке макромолекул увеличивается свободный объем, релакса­ция ускоряется, что приводит к уменьшению σ_в при той же температуре. Это равносильно снижению (d σ_в /dT). Плотность упаковки определяется наличием заместителей, их объемом и расположением, например, для карбоцепных эластомеров она убывает в ряду цис-1,4-полибутадиен, цис-1,4-полиизопрен, со­полимер бутадиена со стиролом, сополимер бутадиена с нит­рилом акриловой кислоты (НАК); в этом же направлении уве­личивается интервал вынужденной высокоэластичности.

Молекулярная масса влияет на Т_с, σ_хр и, следовательно, на Т_хр. Для полимеров, у которых М>>М_сг, Т_с практически от мо­лекулярной массы не зависит, а Т_хр снижается ввиду роста σ_хр (рис. 5.7), что приводит к повышению ∆Т_в.

Таким образом, деформационные свойства полимера в стек­лообразном состоянии можно охарактеризовать модулем упру­гости, пределом вынужденной высокоэластичности, его измене­нием с температурой, величинами упругой и вынужденно-эла­стической деформации.

Дата добавления: 2014-01-05